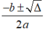Đáp án C
Xét phương trình bậc hai một ẩn và biệt thức
• TH1: Nếu thì phương trình vô nghiệm
• TH2: Nếu thì phương trình có nghiệm kép
x
1
=
x
2
= 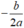
• TH3: Nếu thì phương trình có hai nghiệm phân biệt
x
1
,
2
=