Điều kiện:
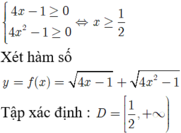
Đạo hàm
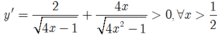
Suy ra hàm số đồng biến trên 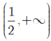
Do đó : phương trình
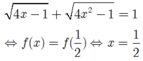
Chọn B.
Điều kiện:
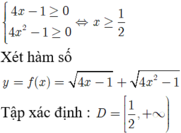
Đạo hàm
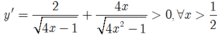
Suy ra hàm số đồng biến trên 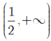
Do đó : phương trình
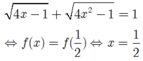
Chọn B.
Cho hàm số f ( x ) = 3 x - 4 + ( x + 1 ) . 2 7 - x - 6 x + 3 . Giả sử m 0 = a b a , b ∈ ℤ , a b l à p h â n s ố t ố i g i ả n là giá trị nhỏ nhất của tham số thực m sao cho phương trình f 7 - 4 6 x - 9 x 2 + 2 m - 1 = 0 có số nghiệm nhiều nhất. Tính giá trị của biểu thức P = a + b 2
A. 11
B. 7
C. -1
D. 9
Biết a b (trong đó a b là phân số tối giản, a , b ∈ N * ) là giá trị thực của tham số m để hàm số y = 2 x 3 - 3 m x 2 - 6 ( 3 m 2 - 1 ) x + 2018 có hai điểm cực trị x1;x2 thỏa mãn x 1 x 2 + 2 ( x 1 + x 2 ) = 1 . Tính P=a+2b.
![]()
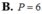
![]()
![]()
Cho phương trình 2 log 4 2 x 2 - x + 2 m - 4 m 2 + log 1 2 x 2 + m x - 2 m 2 = 0 . Biết rằng S = a ; b ∪ c ; d , a < b < c < d là tập hợp các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt x1, x2 thỏa mãn x 1 2 + x 2 2 > 1 . Tính giá trị biểu thức A = a + b + 5c + 2d.
A. A = 1
B. A = 2
C. A = 0
D. A = 3
Phương trình l o g 3 2 x - 1 x - 1 2 = 3 x 2 - 8 x + 5 có hai nghiệm là a và a b (với a , b ∈ ℕ * và a b là phân số tối giản). Giá trị của b là
A. 1
B. 4
C. 2
D. 3
Biết rằng phương trình 9 x 2 - 2 x . 7 x = 7 9 . Có hai nghiệm phân biệt là x1; x2. Tổng x1+x2 có dạng log 9 a b với a ; b nguyên dương và a b là phân số tối giản. Tính S = a + 2b
A. 95
B. 100
C. 36
D. 32
Biết phương trình log 5 2 x + 1 x = 2 log 3 ( x 2 - 1 2 x ) có nghiệm duy nhất x = a + b 2 trong đó a, b là các số nguyên. Hỏi m thuộc khoảng nào dưới đây để hàm số y = m x + a - 2 x - m có giá trị lớn nhất trên đoạn [1; 2] bằng -2
A. m ∈ ( 2 ; 4 )
B. m ∈ ( 4 ; 6 )
C. m ∈ ( 6 ; 7 )
D. m ∈ ( 7 ; 9 )
Phương trình 2 x - 2 = 3 x 2 + 2 x - 8 có một nghiệm dạng x = log a b - 4 với a , b là các số nguyên dương thuộc khoảng 1 ; 5 . Khi đó a + 2 b bằng
![]()
![]()
![]()
![]()
Cho phương trình m - 1 log 1 2 2 x - 2 2 + 4 m - 5 log 1 2 1 ( x - 2 ) + 4 m - 4 = 0 (với m là tham số). Gọi S = a ; b là tập hợp các giá trị của m để phương trình có nghiệm trên đoạn 5 2 ; 4 . Tính a + b .
A. 7 3 .
B. - 2 3 .
C. - 3 .
D. 1034 237 .
Cho hàm số f ( x ) = ln ( 1 - 4 ( 2 x - 1 ) 2 ) . Biết rằng f ( 2 ) + f ( 3 ) + . . . + f ( 2020 ) = ln a b , trong đó a b là phân số tối giản, a , b ∈ N * . Tính b -3a
A. -2
B. 3
C. -1
D. 1