a)
b)
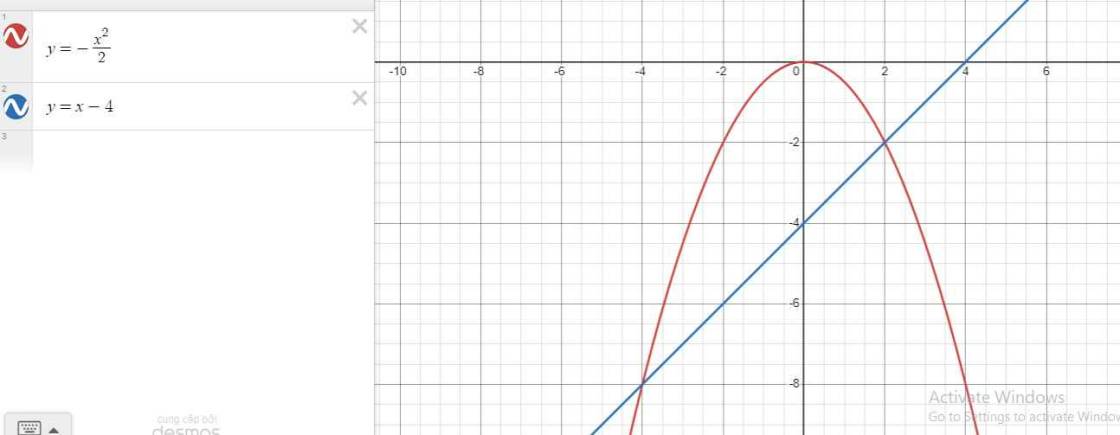
Xét PT hoành độ giao điểm (P) và (d) ta có:
\(-\dfrac{x^2}{2}=x-4\)
\(\Leftrightarrow-\dfrac{x^2}{2}-x+4=0\)
\(\Leftrightarrow x^2+2x-8=0\)
\(\Delta=2^2-4\cdot1\cdot\left(-8\right)=4+32=36>0\)
\(\Rightarrow\) PT có 2 nghiệm phân biệt
\(x_1=\dfrac{-2-\sqrt{36}}{2\cdot1}=\dfrac{-2-6}{2}=-4\)
\(x_2=\dfrac{-2+\sqrt{36}}{2\cdot1}=\dfrac{-2+6}{2}=2\)
Thay x1 vào (d) ta có:
y= -4 - 4 = -8
Thay x1 vào (d) ta có:
y= 2 - 4 = -2
Vậy (P) và (d) cắt nhau tại 2 điểm phân biệt có tọa độ (-4;-8) và (2;-2)
c)
Gọi PT của (d') là y=ax+b
Vì (d')//(d) nên a=1 \(\Rightarrow\) PT của (d') có dạng y=x+b
Thay x=1, y=2 vào (d') y=x+b ta có:
2=1+b
\(\Leftrightarrow\) b=1
Vậy (d') có PT y=x+1 thì song song (d) và đi qua A(1;2)













