Các câu hỏi tương tự
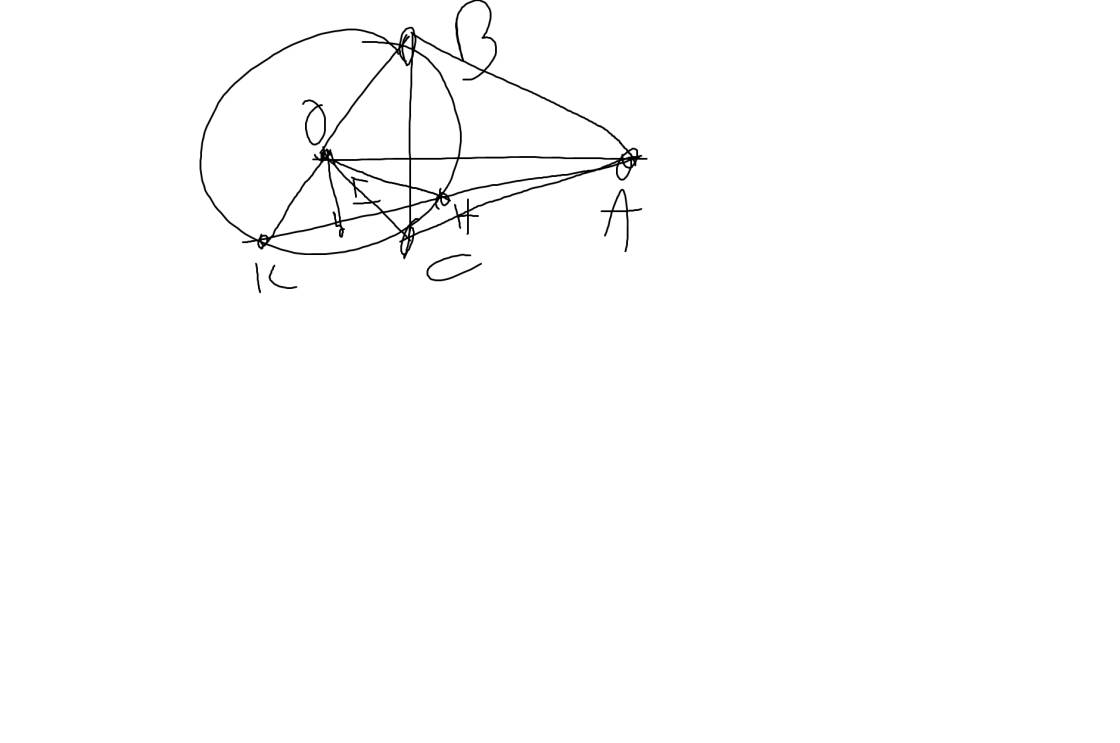
1. Cho (O;R) và điểm A nằm ngoài đường tròn (O). Qua A vẽ đường thẳng d ắt (O) tại H,K (AH,AK). Gọi T là trung điểm HK. Kẻ tiếp tuyến AB, AC (B, C là tiếp điểm, B thuộc cung lớn HK).2. Cho tam giác ABC đều, AD là đường cao. Gọi E là 1 điểm thuộc BD. H là trung điểm AE. Vẽ EF vuông góc với AB tại F, EG vuông góc voies AC tại G.a) CM: ADEF nội tiếp.b) Tính góc DHF.c) Gọi I là giao điểm AE và FG. CM: IA.IE IF.IG3. Cho tam giác ABC nhọn (ABAC, ABBC) có 2 đường cao AH, BK cắt nhau tại Oa) CM: Tứ giá...
Đọc tiếp
1. Cho (O;R) và điểm A nằm ngoài đường tròn (O). Qua A vẽ đường thẳng d ắt (O) tại H,K (AH,AK). Gọi T là trung điểm HK. Kẻ tiếp tuyến AB, AC (B, C là tiếp điểm, B thuộc cung lớn HK).
2. Cho tam giác ABC đều, AD là đường cao. Gọi E là 1 điểm thuộc BD. H là trung điểm AE. Vẽ EF vuông góc với AB tại F, EG vuông góc voies AC tại G.
a) CM: ADEF nội tiếp.
b) Tính góc DHF.
c) Gọi I là giao điểm AE và FG. CM: IA.IE = IF.IG
3. Cho tam giác ABC nhọn (AB<AC, AB<BC) có 2 đường cao AH, BK cắt nhau tại O
a) CM: Tứ giác ABHK nội tiếp.
b) Lấy điểm E đối xứng với A qua K. CMR góc BKH = DEB
c) Vẽ F sao cho tứ giác ABFD là hình bình hành. CMR: BDEC nội tiếp và FE // BD
Cho đường tròn ( O; R ) và điểm A cố định ngoài đường tròn. Qua A kẻ 2 tiếp tuyến AM, AN với đường tròn (M và N là các tiếp điểm). Một đường thẳng d đi qua A cắt (O;R) tại B và C (AB<AC). Gọi I là trung điểm BC
a, Chứng minh A, M, N, O, I cùng thuộc 1 đường tròn
b, Chứng minh AK.AI = AB.AC
Câu 1: Cho (O;R) và điểm A nằm ngoài đường tròn (O). Vẽ 2 tiếp tuyến AB, AC của (O) (B,C: tiếp điểm). Vẽ cát tuyến ADE của (O); D nằm giữa D & E; tia AD nằm giữa 2 tia AB và AO.a) Gọi H là giao điểm của OA và BC. C/m: DEOH nội tiếpb) Đường thẳng AO cắt (O) tại M và N (M nằm giữa A và O). C/m: EH.AD MH.ANCâu 2: Cho nửa đường tròn tâm (O;R) đường kính AB và điểm C trên đường tròn sao cho CACB. Gọi M là trung điểm của dây cung AC. Nối BM cắt cung AC tại E; AE và BC kéo dài cắt nhau tại D.a) C/m: MO...
Đọc tiếp
Câu 1: Cho (O;R) và điểm A nằm ngoài đường tròn (O). Vẽ 2 tiếp tuyến AB, AC của (O) (B,C: tiếp điểm). Vẽ cát tuyến ADE của (O); D nằm giữa D & E; tia AD nằm giữa 2 tia AB và AO.
a) Gọi H là giao điểm của OA và BC. C/m: DEOH nội tiếp
b) Đường thẳng AO cắt (O) tại M và N (M nằm giữa A và O). C/m: EH.AD= MH.AN
Câu 2: Cho nửa đường tròn tâm (O;R) đường kính AB và điểm C trên đường tròn sao cho CA=CB. Gọi M là trung điểm của dây cung AC. Nối BM cắt cung AC tại E; AE và BC kéo dài cắt nhau tại D.
a) C/m: MOCD là hình bình hành
b) Vẽ đường tròn tâm E bán kính EA cắt (O) tại điểm thứ 2 là N. Kẻ EF vuông góc với AC, EF cắt AN tại I, cắt (O) tại điểm thứ 2 là K; EB cắt AN tại H. C/m: BHIK nội tiếp.
Câu 3: Cho (O;R). Từ điểm S nằm ngoài đường tròn sao cho SO=2R. Vẽ tiếp tuyến SA,SB (A,B là tiếp tuyến). Vẽ cát tuyến SDE (D nằm giữa S và E), điểm O nằm trong góc ESB. Từ O kẻ đường vuông góc với OA cắt SB tại M. Gọi I là giao điểm của OS và (O).
a) C/m: MI là tiếp tuyến của (O)
b) Qua D kẻ đường vuông góc với OB cắt AB tại H và EB tại K. C/m: H là trung điểm của DK.
Cho đường tròn (O;R), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn ( B, C là các tiếp điểm), gọi E là trung điểm của BC.1. Cm A, E, O thẳng hàng và OER22. Qua điểm M thuộc cung nhỏ BC kẻ tiếp tuyến với đường tròn (O) , nó cắt các tiếp tuyến AB, AC thứ tự tại D và K. Cm chu vi tam giác ADK bằng 2AB.3. Đường thẳng đi qua O song song BC cắt các đường thẳng AB , AC thứ tự P,Q. Cm DP + KQ PQ
Đọc tiếp
Cho đường tròn (O;R), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn ( B, C là các tiếp điểm), gọi E là trung điểm của BC.
1. Cm A, E, O thẳng hàng và OE=R2
2. Qua điểm M thuộc cung nhỏ BC kẻ tiếp tuyến với đường tròn (O) , nó cắt các tiếp tuyến AB, AC thứ tự tại D và K. Cm chu vi tam giác ADK bằng 2AB.
3. Đường thẳng đi qua O song song BC cắt các đường thẳng AB , AC thứ tự P,Q. Cm DP + KQ >= PQ
Từ điểm M nằm ngoài đường tròn (O;R) kẻ tiếp tuyến MA (A là tiếp điểm) và cát tuyến MBC ko đi qua tâm O (điểm B nằm giữa 2 điểm M và C) gọi H là trung điểm của BC đường thẳng OH cắt (O;R) tại hai điểm N,K ( trong đó điểm K thuộc cung BAC. Gọi D là giao điểm của AN và BC).CM a) tứ giác AKHD là tứ giác nội tiếp b) góc NAB =góc NBD và NB^2 = NA ND
Từ một điểm A nằm ngoài đường tròn (O;R) kẻ tiếp tuyến AB với (O) (B là tiếp điểm). Đường thẳng đi qua B vuông góc với OA tại H và cắt đường trong (O) tại C. Vẽ đường kính BD. Đường thẳng AO cắt đường tròn (O) tại 2 điểm M và N (M nằm giữa A và N). Chứng minh:a) CD//OAb) AC là tiếp tuyến của đường tròn (O)c) Cho biết R 15cm, BC 24CM. Tính AB, OAd) Gọi I là trung điểm của HN. Từ H kẻ đường vuông góc với BI cắt BM tại E. Chứng minh: M là trung điểm của BE.
Đọc tiếp
Từ một điểm A nằm ngoài đường tròn (O;R) kẻ tiếp tuyến AB với (O) (B là tiếp điểm). Đường thẳng đi qua B vuông góc với OA tại H và cắt đường trong (O) tại C. Vẽ đường kính BD. Đường thẳng AO cắt đường tròn (O) tại 2 điểm M và N (M nằm giữa A và N). Chứng minh:
a) CD//OA
b) AC là tiếp tuyến của đường tròn (O)
c) Cho biết R = 15cm, BC = 24CM. Tính AB, OA
d) Gọi I là trung điểm của HN. Từ H kẻ đường vuông góc với BI cắt BM tại E. Chứng minh: M là trung điểm của BE.
cho điểm A nằm ngoài đường tròn (O;R) vẽ các tiếp tuyến AB, AC với đường tròn (o) (B,C là các tiếp điểm) gọi H là giao điểm của OA và BC, điểm M thuộc cung BC, đường thẳng AM cắt đường tròn (O) tại D và E (D nằm giũa A và M), điểm N là trung điểm của dây cung DE1) chứng minh 5 điểm A,B,C,O và N cùng thuộc 1 đường tròn2) chứng minh góc BOC2.ANC và tam giác AMH đồng dạng với tam guacs AON3) chứng minh AB2 AD.AE và tứ giác DHOE là tứ giác nội tiếp
Đọc tiếp
cho điểm A nằm ngoài đường tròn (O;R) vẽ các tiếp tuyến AB, AC với đường tròn (o) (B,C là các tiếp điểm) gọi H là giao điểm của OA và BC, điểm M thuộc cung BC, đường thẳng AM cắt đường tròn (O) tại D và E (D nằm giũa A và M), điểm N là trung điểm của dây cung DE
1) chứng minh 5 điểm A,B,C,O và N cùng thuộc 1 đường tròn
2) chứng minh góc BOC=2.ANC và tam giác AMH đồng dạng với tam guacs AON
3) chứng minh AB2= AD.AE và tứ giác DHOE là tứ giác nội tiếp
Cho đường tròn (O; R) và điểm S cố định nằm ngoài đường tròn (O). Kẻ hai tiếp tuyến SA và SB của đường tròn (O; R)(A, B là tiếp điểm). Đường thẳng bất kỳ qua S cắt đường tròn (O) tại C và D(SC < SD và C, O, D không thẳng hàng). Gọi E là trung điểm của đoạn thẳng CD. 1 Chứng minh bốn điểm S, A, 0, B cùng thuộc một đường tròn.
Mik cần hình và phần giải câu a
Câu 4: (3,0 điểm). Cho đường tròn tâm O bán kính R và một điểm M nằm ngoài đường tròn. Qua M kẻ tiếp tuyến MA với đường tròn (A là tiếp điểm). Tia Mx nằm giữa MA và MO cắt đường tròn (O; R) tại hai điểm C và D (C nằm giữa M và D). Gọi I là trung điểm của dây CD, kẻ AH vuông góc với MO tại H. a/ Tính OH. OM theo R. b/ Chứng minh: Bốn điểm M, A, I , O cùng thuộc một đường tròn. c/ Gọi K là giao điểm của OI với HA. Chứng minh KC là tiếp tuyến của đường tròn (O; R)
Đọc tiếp
Câu 4: (3,0 điểm). Cho đường tròn tâm O bán kính R và một điểm M nằm ngoài đường tròn. Qua M kẻ tiếp tuyến MA với đường tròn (A là tiếp điểm). Tia Mx nằm giữa MA và MO cắt đường tròn (O; R) tại hai điểm C và D (C nằm giữa M và D). Gọi I là trung điểm của dây CD, kẻ AH vuông góc với MO tại H. a/ Tính OH. OM theo R. b/ Chứng minh: Bốn điểm M, A, I , O cùng thuộc một đường tròn. c/ Gọi K là giao điểm của OI với HA. Chứng minh KC là tiếp tuyến của đường tròn (O; R)
Cho đường tròn tâm (O) cố định . Từ một điểm A cố định ở bên ngoài đường tròn (O) kẻ các tiếp tuyến AM và An với đường tròn ( M và N là các tiếp điểm ) đường thẳng qua A cắt đường tròn tâm (O) tại hai điểm B và C ( B nằm giữa A và C ) gọi I là trung điểm BC . a, chứng minh tứ giác amon nội tiếp. b, gọi k là giao điểm của MN và BC . chứng minh tam giác AKM đồng dạng tam giác AMI và AK.AIAB.AC
Đọc tiếp
Cho đường tròn tâm (O) cố định . Từ một điểm A cố định ở bên ngoài đường tròn (O) kẻ các tiếp tuyến AM và An với đường tròn ( M và N là các tiếp điểm ) đường thẳng qua A cắt đường tròn tâm (O) tại hai điểm B và C ( B nằm giữa A và C ) gọi I là trung điểm BC . a, chứng minh tứ giác amon nội tiếp.
b, gọi k là giao điểm của MN và BC . chứng minh tam giác AKM đồng dạng tam giác AMI và AK.AI=AB.AC