 a) Ta có:
a) Ta có:
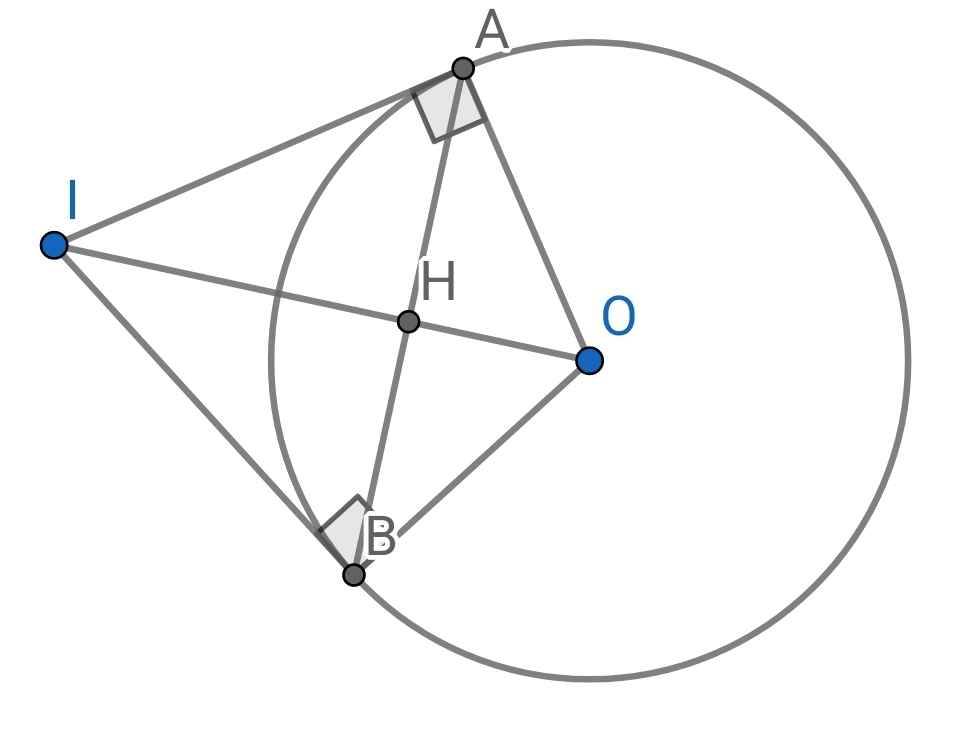
IA = IB (tính chất hai tiếp tuyến cắt nhau)
⇒ I nằm trên đường trung trực của AB (1)
OA = OB (bán kính)
⇒ O nằm trên đường trung trực của AB (2)
Từ (1) và (2) ⇒ OI là đường trung trực của AB
Mà H là giao điểm của AB và OI
⇒ H là trung điểm của AB
⇒ AH = AB : 2 = 24 : 2 = 12 (cm)
Do OI là đường trung trực của AB (cmt)
⇒ AH ⊥ OI
⇒ AH ⊥ HI
∆AHI vuông tại H
⇒ AI² = AH² + IH² (Pytago)
⇒ IH² = AI² - AH²
= 20² - 12²
= 256
⇒ IH = 16 (cm)
∆OAI vuông tại A có AH là đường cao
⇒ AH² = IH.OH
⇒ OH = AH² : IH
= 12² : 16
= 9 (cm)
b) Bán kính của (O) là đoạn OA
Ta có:
OI = OH + IH = 9 + 16 = 25 (cm)
∆OAI vuông tại A
⇒ OI² = IA² + OA² (Pytago)
OA² = OI² - IA²
= 25² - 20²
= 225
⇒ OA = 15 (cm)
Vậy bán kính OA = 15 cm
Để giải bài toán này, chúng ta có thể sử dụng các định lý về tiếp tuyến và đường tròn. Dưới đây là cách giải từng phần của bài toán:
a) Để tính độ dài AH, IH và OH, chúng ta cần sử dụng định lý về tiếp tuyến và đường tròn.
Theo định lý tiếp tuyến, ta có:
AH^2 = AI * AB
AH^2 = 20cm * 24cm
AH^2 = 480cm^2
AH = √480cm ≈ 21.91cm
Theo định lý tiếp tuyến, ta cũng có:
IH^2 = IB * AB
IH^2 = 20cm * 24cm
IH^2 = 480cm^2
IH = √480cm ≈ 21.91cm
Để tính OH, chúng ta cần sử dụng định lý về trung điểm. Vì O là trung điểm của đoạn thẳng IH, nên ta có:
OH = 1/2 * IH
OH = 1/2 * 21.91cm
OH ≈ 10.96cm
Vậy, độ dài AH là khoảng 21.91cm, độ dài IH là khoảng 21.91cm và độ dài OH là khoảng 10.96cm.
b) Để tính bán kính (o), chúng ta có thể sử dụng định lý về đường tròn ngoại tiếp.
Theo định lý đường tròn ngoại tiếp, ta có:
R = AI = 20cm
Vậy, bán kính (o) là 20cm.














