Các câu hỏi tương tự
Cho nửa đường tròn (O) đường kính AB 2R. Gọi (d) là tiếp tuyến của (O) tại B. Trên cùng AB lấy điểm M tuỳ ý (M không trùng với A và B), tía AM cắt (d) tại điểm N. Gọi C là trung điểm của AM, tia CO cắt (d) tại điểm D1. Chứng minh OBNC là tứ giác nội tiếp.2. Chứng minh: ON ⊥ AD và CA. CN CO. CD3. Xác định vị trí điểm M trên cung AB để tổng AN +2AM đạt giá trị nhỏ nhất.
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB= 2R. Gọi (d) là tiếp tuyến của (O) tại B. Trên cùng AB lấy điểm M tuỳ ý (M không trùng với A và B), tía AM cắt (d) tại điểm N. Gọi C là trung điểm của AM, tia CO cắt (d) tại điểm D
1. Chứng minh OBNC là tứ giác nội tiếp.
2. Chứng minh: ON ⊥ AD và CA. CN = CO. CD
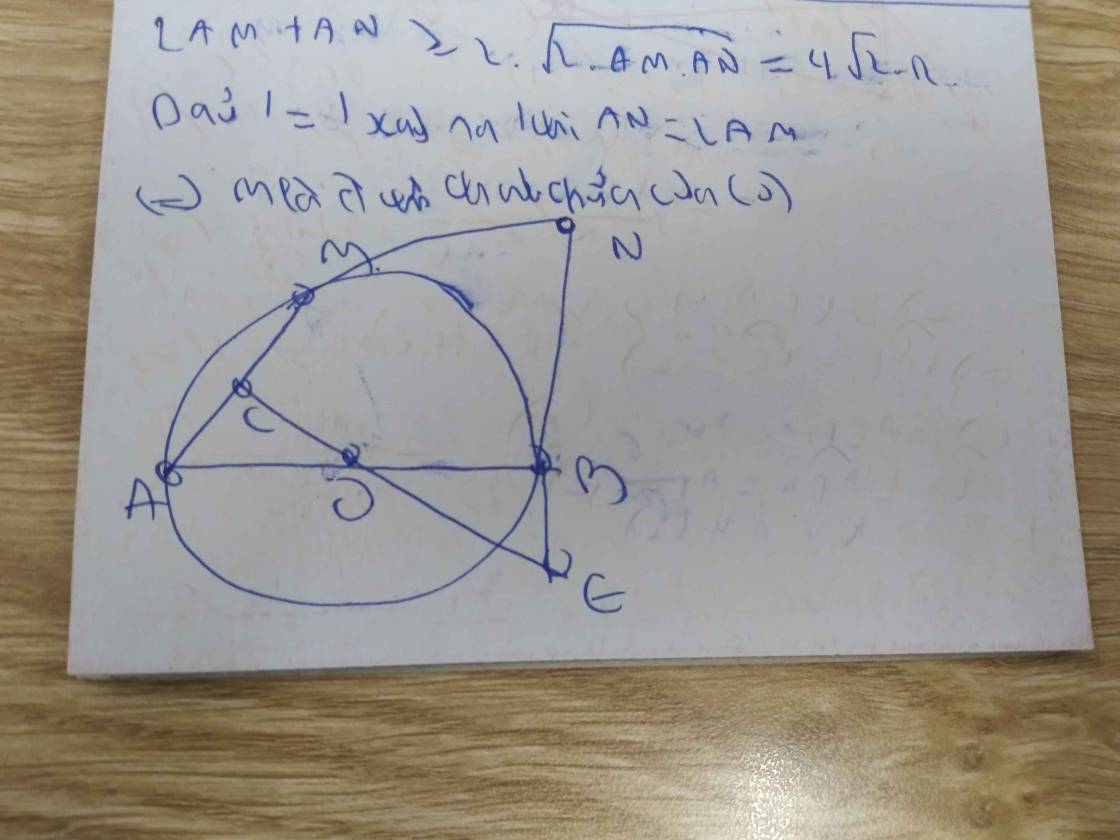
3. Xác định vị trí điểm M trên cung AB để tổng AN +2AM đạt giá trị nhỏ nhất.
Cho nửa đường tròn tâm (O) đường kính AB2R. Vẽ đường thẳng d là tiếp tuyến của (O) tại B. Trên cung AB lấy điểm M tùy ý (M khác A và B), tia AM cắt d tại N. Gọi C là trung điểm của AM, tai CO cắt d tại D.a) Chứng minh rằng: OBNC nội tiếp.b)Chứng minh rằng: NO⊥ADc)Chứng minh rằng: CA.CNCO.CDd)Xác định vị trí điểm M để (2AMAN) đạt giá trị nhỏ nhất
Đọc tiếp
Cho nửa đường tròn tâm (O) đường kính AB=2R. Vẽ đường thẳng d là tiếp tuyến của (O) tại B. Trên cung AB lấy điểm M tùy ý (M khác A và B), tia AM cắt d tại N. Gọi C là trung điểm của AM, tai CO cắt d tại D.
a) Chứng minh rằng: OBNC nội tiếp.
b)Chứng minh rằng: NO⊥AD
c)Chứng minh rằng: CA.CN=CO.CD
d)Xác định vị trí điểm M để (2AM=AN) đạt giá trị nhỏ nhất
Bài 5: Cho nửa đường tròn (O) đường kính AB = 2R. Gọi M là một điểm thay đổi trên tiếp tuyến Bx của (O). Nối AM cắt (O) tại N. Gọi I là trung điểm của AN.
a) Chứng minh: ΔAIO ∼ ΔBMN ; ΔOBM ∼ ΔINB
b) Tìm vị trí của điểm M trên tia Bx để diện tích ΔAIO có giá trị lớn nhất.
cho nửa đtòn (O) đường kính ab2r.Điểm m di chuyển trên nửa đtròn(M khác A và B)C là trung điểm của dây cung am.Đường thẳng d là tiếp tuyến với nửa đtròn tại b.tia am cắt d tại điểm n. đường thẳng oc cắt d tại e a,Chứng minh:tứ giác ocnb nội tiếp b,Chứng minh:ac.anao.abc,Chứng minh no vuông góc với aed,Tìm vị trí điểm m sao cho(2.am+an)nhỏ nhất Vẽ hình làm cả 4 câu giúp e với ạ
Đọc tiếp
cho nửa đtòn (O) đường kính ab=2r.Điểm m di chuyển trên nửa đtròn(M khác A và B)C là trung điểm của dây cung am.Đường thẳng d là tiếp tuyến với nửa đtròn tại b.tia am cắt d tại điểm n. đường thẳng oc cắt d tại e
a,Chứng minh:tứ giác ocnb nội tiếp
b,Chứng minh:ac.an=ao.ab
c,Chứng minh no vuông góc với ae
d,Tìm vị trí điểm m sao cho(2.am+an)nhỏ nhất
Vẽ hình làm cả 4 câu giúp e với ạ
cho nửa đường tròn O đường kính AB kẻ tiếp tuyến bx tại b của O Gọi M là điểm di động thuộc nửa đường tròn (O) và AM cắt Bx tại N.Xác định vị trí của M để 2AM+AN nhỏ nhất
cho nữa đường tròn (O) đường kính MN=2R. gọi (d) là tiếp tuyến của (O) tại N. trên cung MN lấy điểm E tùy ý (E không trùng M, N), tia ME cắt (d) tại F. gọi P là trung điểm của ME, tia PO cắt (d) tại Q. Xác định vị trí điểm E trên cung MN để tổng MF+2ME đạt giá trị nhỏ nhất
): Cho đoạn thẳng AB 2a có trung điểm O . Trên cùng một nửa mặt phẳng bờ AB , dựng nửa đường tròn (O,AB) và ( O’,AO) , Trên (O’) lấy M ( M ≠ A, M ≠ O ). Tia OM cắt (O) tại C . Gọi D là giao điểm thứ hai của CA với (O’). a/ Chứng minh rằng tam giác AMD cân . b/ Tiếp tuyến C của (O) cắt tia OD tại E. Xác định vị trí tương đối của đương thẳng EA đối với (O) và (O’). c/ Đường thẳng AM cắt OD tại H, đường tròn ngoại tiếp tam giác COH cắt (O) tại điểm thứ hai là N. Chứng minh ba điểm A, M, N thẳng hà...
Đọc tiếp
): Cho đoạn thẳng AB = 2a có trung điểm O . Trên cùng một nửa mặt phẳng bờ AB , dựng nửa đường tròn (O,AB) và ( O’,AO) , Trên (O’) lấy M ( M ≠ A, M ≠ O ). Tia OM cắt (O) tại C . Gọi D là giao điểm thứ hai của CA với (O’). a/ Chứng minh rằng tam giác AMD cân . b/ Tiếp tuyến C của (O) cắt tia OD tại E. Xác định vị trí tương đối của đương thẳng EA đối với (O) và (O’). c/ Đường thẳng AM cắt OD tại H, đường tròn ngoại tiếp tam giác COH cắt (O) tại điểm thứ hai là N. Chứng minh ba điểm A, M, N thẳng hàng. d/ Tại vị trí của M sao cho ME // AB hãy tính OM theo a .
Cho đường tròn (O;R) đường kính AB. Gọi M là điểm bất kì trên (O), AM cắt tiếp tuyến B của đường tròn (O) tại C. Tìm vị trí M để 2AM+AC min
1. Từ A ngoài đường tròn tâm O. Kẻ 2 tia tiếp tuyến AM , AN. Biết góc MAN a độ ( không đổi ). Từ I bất kì trên cung nhỏ MN, vẽ tiếp tuyến cắt AM , AN tại B và C. OB và OC cắt đường tròn O tại D và E. CM : Cung DE không đổi khi I chạy trên cung MN2. Cho đường tròn O và O cắt nhau tại A và B. Qua A kẻ đường thẳng vuông góc với AB cắt đường tròn O tại C, cắt đường tròn O tại D. Tia CB cắt đường tròn O tại F , tia DB cắt đường tròn O tại E. CM : AB là tia phân giác góc EAF3. Cho tam giác ABC nhọn....
Đọc tiếp
1. Từ A ngoài đường tròn tâm O. Kẻ 2 tia tiếp tuyến AM , AN. Biết góc MAN = a độ ( không đổi ). Từ I bất kì trên cung nhỏ MN, vẽ tiếp tuyến cắt AM , AN tại B và C. OB và OC cắt đường tròn O tại D và E. CM : Cung DE không đổi khi I chạy trên cung MN
2. Cho đường tròn O và O' cắt nhau tại A và B. Qua A kẻ đường thẳng vuông góc với AB cắt đường tròn O tại C, cắt đường tròn O' tại D. Tia CB cắt đường tròn O' tại F , tia DB cắt đường tròn O tại E. CM : AB là tia phân giác góc EAF
3. Cho tam giác ABC nhọn. Điểm I bất kì trong tam giác. Kẻ IH vuông góc AB , IK vuông góc AC , IL vuông góc AB. Tìm vị trí điểm I sao cho : AL^2 + BH^2 + CK^2 đạt gtnn