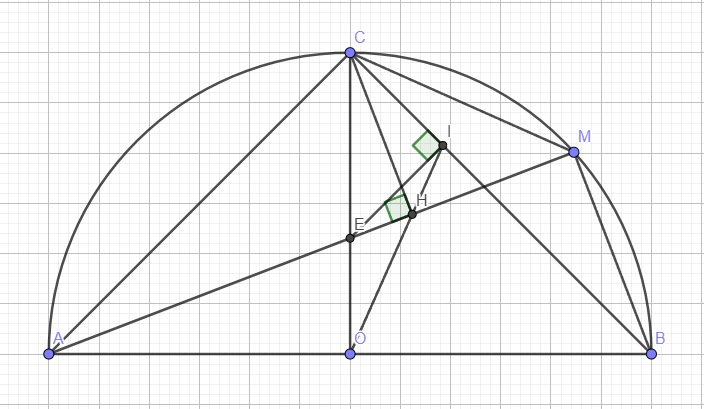
Cho nửa đường tròn(O) đường kính AB. C là điểm chính giữa cung AB .Trên cung nhỏ BC lấy điểm M(M khác B,C). Gọi H là hình chiếu vuông góc của C lên AM ,E là giao điểm của OC và AM.
a. Chứng minh tam giác ABC vuông cân
b. Chứng minh tứ giác AOHC nội tiếp
c. Chứng minh hai tam giác OCH và BCM đồng dạng
d. Gọi I là hình chiếu của E lên BC. Chứng minh 3 điểm O,H,I thẳng hàng
a.
Do C là điểm chính giữa cung AB \(\Rightarrow sđ\stackrel\frown{AC}=sđ\stackrel\frown{BC}\)
\(\Rightarrow\widehat{CAB}=\widehat{CBA}\) (hai góc nt chắn 2 cung bằng nhau)
\(\Rightarrow\Delta ABC\) cân tại C (1)
Lại có AB là đường kính \(\Rightarrow\widehat{ACB}=90^0\) (góc nt chắn nửa đường tròn) (2)
(1);(2) \(\Rightarrow\Delta ABC\) vuông cân tại C
b.
Do O là trung điểm AB và tam giác ABC cân tại C \(\Rightarrow CO\) vừa là trung tuyến vừa là đường cao
\(\Rightarrow CO\perp AB\)
\(\Rightarrow\widehat{COA}=\widehat{CHA}=90^0\)
\(\Rightarrow O,H\) cùng nhìn AC dưới 1 góc vuông nên AOHC nội tiếp
c.
Do AOHC nội tiếp \(\Rightarrow\widehat{OCH}=\widehat{OAH}\) (cùng chắn OH)
Mà \(\widehat{OAH}=\widehat{BCM}\) (cùng chắn BM của (O))
\(\Rightarrow\widehat{OCH}=\widehat{BCM}\) (3)
Cũng do AOHC nội tiếp \(\Rightarrow\widehat{COH}=\widehat{CAH}\) (cùng chắn CH)
Lại có \(\widehat{CAH}=\widehat{CBM}\) (cùng chắn CM của (O))
\(\Rightarrow\widehat{COH}=\widehat{CBM}\) (4)
(3);(4) \(\Rightarrow\Delta OCH\sim\Delta BCM\left(g.g\right)\)
d.
EI vuông góc BC \(\Rightarrow I,H\) cùng nhìn CE dưới 1 góc vuông
\(\Rightarrow CIHE\) nội tiếp \(\Rightarrow\widehat{ECI}+\widehat{IHE}=180^0\) (5)
\(\Delta ABC\) cân tại C theo cm câu a \(\Rightarrow CO\) vừa là trung tuyến vừa là phân giác
\(\Rightarrow\widehat{ECI}=\widehat{ACO}\)
Theo câu b, AOCH nội tiếp \(\Rightarrow\widehat{ACO}=\widehat{AHO}\) (cùng chắn AO)
\(\Rightarrow\widehat{ECI}=\widehat{AHO}\) (6)
(5);(6) \(\Rightarrow\widehat{EHI}+\widehat{AHO}=180^0\)
\(\Rightarrow O,H,I\) thẳng hàng