Cho đường tròn (O; R) có đường kính AB. Bán kính CO vuông góc với AB. M là một điẻm bất kỳ trên cung nhỏ AC (M khác A, C), BM cắt AC tại H. Gọi K là hình chiếu của H trên AB
a, Chứng minh CBKH là tứ giác nội tiếp
b, Chứng minh: A C M ^ = A C K ^
c, Trên đoạn thẳng BM lấy điểm E sao cho BE = AM. Chứng minh tam giác ECM là tam giác vuông cân tại C
d, Gọi d là tiếp tuyến của (O) tại điểm A; cho P là điểm nằm trên d ao cho hai điểm P, C nằm trong cùng một nưanr mặt phẳng bờ AB và A P . M B M A = R . Chứng minh đường thẳng PB đi qua trung điểm của đoạn thẳng HK
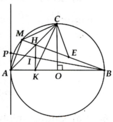
a, Chứng minh được H C B ^ = H K B ^ = 90 0
b, A C K ^ = H B K ^ (CBKH nội tiếp)
Lại có: A C M ^ = H B K ^ = 1 2 s đ A M ⏜
=> A C M ^ = A C K ^
c, Chứng minh được:
DMCA = DECB (c.g.c) => MC = CE
Ta có: C M B ^ = C A B ^ = 1 2 s đ C B ⏜ = 45 0
=> DMCE vuông cân tại C
d, Gọi P B ∩ H K = I
Chứng minh được DHKB đồng dạng với DAMB (g.g)
=> H K K B = M A M B = A P R => H K = A P . B K R
Mặt khác: ∆BIK:∆BPA(g.g) => (ĐPCM)











