Cho nửa đường tròn tâm O có đường kính AB . Vẽ các tiếp tuyến Ax, By là các tia vuông góc với AB ( Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB ). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C, D. a. Chứng minh rằng: đường tròn đường kính CD tiếp xúc với AB . b. Tìm vị trí của điểm M để hình thang ABDC có chu vi nhỏ nhất. c. Tìm vị trí của C, D để hình thang ABDC có chu vi bằng 14cm . Biết AB = 4cm .
a: Gọi H là trung điểm của CD
=>H là tâm đường tròn đường kính CD
Xét (O) có
CM,CA là các tiếp tuyến
Do đó: CM=CA và OC là phân giác của góc MOA
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc MOB
ta có: OC là phân giác của góc MOA
=>\(\hat{MOA}=2\cdot\hat{MOC}\)
ta có: OD là phân giác của góc MOB
=>\(\hat{MOB}=2\cdot\hat{MOD}\)
ta có: \(\hat{MOA}+\hat{MOB}=180^0\) (hai góc kề bù)
=>\(2\left(\hat{MOC}+\hat{MOD}\right)=180^0\)
=>\(2\cdot\hat{COD}=180^0\)
=>\(\hat{COD}=90^0\)
=>O nằm trên đường tròn đường kính CD
hay O nằm trên (H)
Xét hình thang ABDC có
O,H lần lượt là trung điểm của AB,CD
=>OH là đường trung bình của hình thang ABDC
=>OH//AC//BD và \(OH=\frac{AC+BD}{2}\)
ta có: OH//AC
CA⊥AB
Do đó: OH⊥AB
=>(H) tiếp xúc với AB tại O
b: \(C_{ABDC}=AC+CD+DB+AB\)
=CM+CD+DM+AB
=CD+CD+AB
=2CD+AB
Kẻ CK⊥BD tại K
=>CK<=CD
CK⊥BD
AB⊥BD
Do đó: CK//AB
Xét tứ giác ABKC có
KC//AB
AC//BK
Do đó: ABKC là hình bình hành
=>KC=AB=2R
Để chu vi hình thang ABDC nhỏ nhất thì 2CD+AB nhỏ nhất
mà AB cố định
nên 2CD nhỏ nhất
=>CD nhỏ nhất
mà CD<=CK=2R
nên CD nhỏ nhất khi CD=2R
mà OM=R
nên OM=1/2CD
ΔCOD vuông tại O
mà OH là đường trung tuyến
nên \(OH=\frac12CD\)
=>OM=OH
=>M trùng với H
=>MO⊥AB tại O
=>M là điểm chính giữa của cung AB
c: \(C_{ABDC}=2CD+AB\)
=>2CD+4=14
=>2CD=10
=>CD=5(cm)
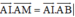và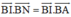 
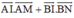theo R.
