Chọn D.
Phương pháp:

Cách giải:
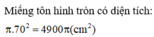
Gọi bán kính đáy và chiều cao của hình nón lần lượt là r , h ( r , h > 0 ) .

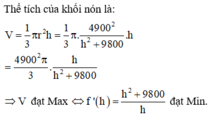
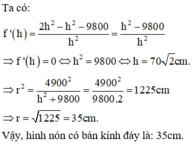
Chọn D.
Phương pháp:

Cách giải:

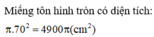
Gọi bán kính đáy và chiều cao của hình nón lần lượt là r , h ( r , h > 0 ) .

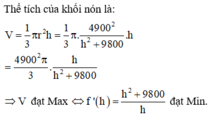
Cho một miếng tôn hình tròn tâm O, bán kính R. Cắt bỏ một phần miếng tôn theo một hình quạt OAB và gò phần còn lại thành một hình nón đỉnh O không có đáy (OA trùng với OB). Gọi S và S ' lần lượt là diện tích của miếng tôn hình tròn ban đầu và diện tích của miếng tôn còn lại. Tìm tỉ số S S ' để thể tích của khối nón đạt giá trị lớn nhất
A. 2 3
B. 1 4
C. 1 3
D. 6 3
Cho một miếng tôn hình tròn tâm O, bán kính R. Cắt bỏ một phần miếng tôn theo một hình quạt OAB và gò phần còn lại thành một hình nón đỉnh O không có đáy (OA trùng với OB). Gọi S và S ' lần lượt là diện tích của miếng tôn hình tròn banđầu và diện tích của miếng tôn còn lại. Tìm tỉ số S ' S để thể tích của khối nón đạt giá trị lớn nhất
A. 2 2
B. 1 4
C. 1 3
D. 6 3
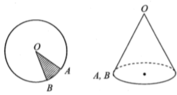
Cho miếng tôn hình tròn tâm O bán kính R. Cắt bỏ một phần miếng tôn theo một hình quạt OAB và gò phần còn lại thành một hình nón đỉnh O hông đáy (OA trùng với OB). Gọi S, S’ lần lượt là diện tích của miếng tôn hình tròn ban đầu và diện tích của miếng tôn còn lại. Tìm tỉ số S ' S để thể tích khối nón lớn nhất
A. 6 3
B. 1 4
C. 2 3
D. 1 3
Với một miếng tôn hình tròn có bán kính bằng R=9cm. Người ta muốn làm một cái phễu bằng cách cắt đi một hình quạt của hình tròn này và gấp phần còn lại thành hình nón (như hình vẽ). Hình nón có thể tích lớn nhất khi độ dài cung tròn của hình quạt tạo thành hình nón bằng
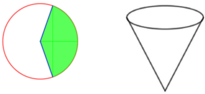
A. 8 π 6 c m
B. 2 π 6 c m
C. π 6 c m
D. 6 π 6 c m
Một phần dụng cụ gồm một phần có dạng trụ, phần còn lại có dạng nón. một hình trụ, đường kính đáy 1,4m, chiều cao 70cm, và một hình nón, bán kính đáy bằng bán kính hình trụ, chiều cao hình nón bằng 0,9m (Các kích thước cho trên hình 100). Khi đó diện tích mặt ngoài của dụng cụ (Không tính nắp đậy) có giá trị gần nhất với:
A. 5,58
B.6,13
C. 4,86
D. 6,36
Một phễu gồm một phần có dạng trụ, phần còn lại có dạng nón. Một hình trụ, đường kính đáy 1,4m, chiều cao 70cm, và một hình nón, bán kính đáy bằng bán kính hình trụ, chiều cao hình nón bằng 0,9m. Khi đó diện tích mặt ngoài của dụng cụ (Không tính nắp đậy) có giá trị gần nhất với:
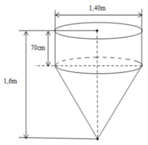
A. 5,58
B. 6,13
C. 4,68
D. 5,53
Hình nón có bán kính đáy r = 3 cm và đường sinh l = 4 cm. Khi đó diện tích toàn phần S t p của hình nón là
A. S t p = 12 π c m 2
B. S t p = 21 π c m 2
C. S t p = 18 π c m 2
D. S t p = 30 π c m 2
Hình nón có bán kính đáy r = 3 cm và đường sinh l = 4 cm. Khi đó diện tích toàn phần S t p của hình nón là
A. S t p = 12 π c m 2 .
B. S t p = 21 π c m 2 .
C. S t p = 18 π c m 2 .
D. S t p = 30 π c m 2 .
Cho hình nón tròn xoay có đường cao h = 20 cm, bán kính đáy r = 25 cm.
a) Tính diện tích xung quanh của hình nón đã cho.
b) TÍnh thể tích của khối nón được tạo bởi hình nón đó.
c) Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12 cm. Tính diện tích thiết diện đó.