Đáp án C
Phương pháp: Gọi là tâm hình vuông ⇒ I ∈ O O ' .
Sử dụng định lý Py-ta-go trong tam giác vuông để tính AB.
Cách giải:
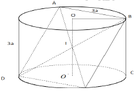
Ta có: I B = O I 2 + O B 2 = 9 a 2 4 + 9 a 2 = 3 a 5 2
⇒ A B = B I . 2 = 3 a 10 2
Đáp án C
Phương pháp: Gọi là tâm hình vuông ⇒ I ∈ O O ' .
Sử dụng định lý Py-ta-go trong tam giác vuông để tính AB.
Cách giải:

Ta có: I B = O I 2 + O B 2 = 9 a 2 4 + 9 a 2 = 3 a 5 2
⇒ A B = B I . 2 = 3 a 10 2
Cho một hình trụ có chiều cao và bán kính đều bằng a. Một hình vuông ABCD có hai cạnh AB, CD lần lượt là hai dây cung của hai đường tròn đáy, cạnh AD, BC không phải là đường sinh của hình trụ. Tính cạnh của hình vuông này
A. a
B. 2a
C. a 5 2
D. a 10 2
Cho một hình trụ có chiều cao và bán kính đều bằng a. Một hình vuông ABCD có hai cạnh AB, CD lần lượt là hai dây cung của hai đường tròn đáy, cạnh AD, BC không phải là đường sinh của hình trụ. Tính cạnh của hình vuông này.
A. a
B. 2a
C. a 10 2
D. a 5 2
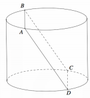
Cho hình trụ (T) có diện tích đáy bằng 48 π và hai dây cung AB,CD lần lượt nằm trên hai đường tròn đáy của (T) sao cho ABCD là một hình vuông có độ dài cạnh bằng 10 và các cạnh của hình vuông này không song song với đường sinh của (T) (tham khảo hình vẽ bên). Tính thể tích của khối trụ (T).
A. 288 π
B. 96 2 π
C. 192 2 π
D. 384 π
Một hình trụ có bán kính đáy bằng chiều cao và bằng a. Một hình vuông ABCD có AB;CD là 2 dây cung của 2 đường tròn đáy và mặt phẳng (ABCD) không vuông góc với đáy. Diện tích hình vuông đó bằng .
A. 5 a 2 4
B. 5 a 2 2 4
C. 5 a 2
D. 5 a 2 2
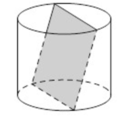
Một chiếc hộp hình trụ với bán kính đáy bằng chiều cao và bằng 10 cm. Một học sinh bỏ một miếng bìa hình vuông vào chiếc hộp đó và thấy hai cạnh đối diện của miếng bìa lần lượt là các dây cung của hai đường tròn đáy hộp và miếng bìa không song song với trục của hộp. Hỏi diện tích của miếng bìa đó bằng bao nhiêu
A. 150 c m 3
B. 250 c m 3
C. 200 c m 3
D. 300 c m 3
Một hình trụ có chiều cao h=2, bán kính đáy r=3. Một mặt phẳng (P) không vuông góc với đáy của hình trụ, lần lượt cắt hai đáy theo các đoạn giao tuyến AB và CD sao cho tứ giác ABCD là hình vuông. Tính diện tích S của hình vuông ABCD
A. S=12ᴨ
B. S=12
C. S=20
D. S=20ᴨ
Cho hình trụ (T)có bán kính bằng 4 cm mặt phẳng (P) cắt hai đáy của hình trụ theo hai dây AB và CD, AB = CD = 5 cm. Tứ giác ABCD là hình chữ nhật AD và BC không là đường sinh,góc giữa mp (P) và mặt phẳng chứa đáy của hình trụ bằng 60 ° . Thể tích của khối trụ là:
A. 60 π 3 cm 3
B. 24 π 13 cm 3
C. 16 π 13 cm 3
D. 48 π 13 cm 3
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh a, AA’ = 2a. Một hình trụ có hai đáy là hai hình tròn lần lượt ngoại tiếp hình vuông ABCD và hình vuông A’B’C’D’. Tính diện tích xung quanh S x q của hình trụ đó
A. S x q = 2 πa 2
B. S x q = 2 πa 2 2
C. S x q = 4 πa 2 2
D. S x q = πa 2 2
Cho hình chóp S.ABC có đường cao SA = h và đáy ABC là tam giác vuông cạnh huyền BC = a. Một mặt trụ đi qua hai điểm B, C và có một đường sinh là SA. Khi đó bán kính mặt trụ bằng
A. a
B. a 2 + h 2
C. ah
D. a 2