Các câu hỏi tương tự
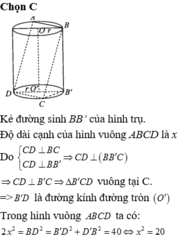
Một hình trụ có bán kính đáy bằng chiều cao và bằng a. Một hình vuông ABCD có AB;CD là 2 dây cung của 2 đường tròn đáy và mặt phẳng (ABCD) không vuông góc với đáy. Diện tích hình vuông đó bằng . A.
5
a
2
4
B.
5
a
2
2...
Đọc tiếp
Một hình trụ có bán kính đáy bằng chiều cao và bằng a. Một hình vuông ABCD có AB;CD là 2 dây cung của 2 đường tròn đáy và mặt phẳng (ABCD) không vuông góc với đáy. Diện tích hình vuông đó bằng .
A. 5 a 2 4
B. 5 a 2 2 4
C. 5 a 2
D. 5 a 2 2
Khi cắt mặt cầu S (O, R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O, R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S (O, R) để khối trụ có thể tích lớn nhất. A.
r...
Đọc tiếp
Khi cắt mặt cầu S (O, R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O, R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R = 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S (O, R) để khối trụ có thể tích lớn nhất.
A. r = 3 2 ; h = 6 2
B. r = 6 2 ; h = 3 2
C. r = 6 3 ; h = 3 3
D. r = 3 3 ; h = 6 3
Một hình nón có chiều cao
S
O
50
c
m
và có bán kính đáy bằng
10
c
m
.
Lấy điểm M thuộc đoạn SO sao cho
O
M
20
c
m
.
Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn
C
. Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi
C...
Đọc tiếp
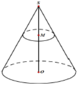
Một hình nón có chiều cao S O = 50 c m và có bán kính đáy bằng 10 c m . Lấy điểm M thuộc đoạn SO sao cho O M = 20 c m . Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn C . Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi C (xem hình vẽ).
A. 16 π 26 c m 2
B. 26 π 26 c m 2
C. 36 π 26 c m 2
D. 46 π 26 c m 2
Cho hình trụ có trục
O
O
, bán kính đáy r và chiều cao
h
3
r
2
.
Hai điểm M, N di động trên đường tròn đáy (O) sao cho OMN là tam giác đều. Gọi H là hìn chiếu vuông góc của O trên mặt phẳng (
O
M
N
). Khi M, N di động trên đường tròn (O) thì đoạn thẳng OH tạo thành mặt xung quanh của một hình nón, tính diện tích S của mặ...
Đọc tiếp
Cho hình trụ có trục O O ' , bán kính đáy r và chiều cao h = 3 r 2 . Hai điểm M, N di động trên đường tròn đáy (O) sao cho OMN là tam giác đều. Gọi H là hìn chiếu vuông góc của O trên mặt phẳng ( O ' M N ). Khi M, N di động trên đường tròn (O) thì đoạn thẳng OH tạo thành mặt xung quanh của một hình nón, tính diện tích S của mặt này.
A. S = 9 3 π r 2 32
B. S = 9 3 π r 2 16
C. S = 9 π r 2 32
D. S = 9 π r 2 16
Cho hình vuông ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của AB và CD. Khi quay hình vuông ABCD quanh MN thành một hình trụ. Gọi (S) là mặt cầu có diện tích bằng diện tích toàn phần của hình trụ, ta có bán kính của mặt cầu (S) là: A.
a
6
3
B.
a
6
2
C.
a...
Đọc tiếp
Cho hình vuông ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của AB và CD. Khi quay hình vuông ABCD quanh MN thành một hình trụ. Gọi (S) là mặt cầu có diện tích bằng diện tích toàn phần của hình trụ, ta có bán kính của mặt cầu (S) là:
A. a 6 3
B. a 6 2
C. a 6 4
D. a 6
Cho hình trụ (T)có bán kính bằng 4 cm mặt phẳng (P) cắt hai đáy của hình trụ theo hai dây AB và CD, AB CD 5 cm. Tứ giác ABCD là hình chữ nhật AD và BC không là đường sinh,góc giữa mp (P) và mặt phẳng chứa đáy của hình trụ bằng
60
°
. Thể tích của khối trụ là: A.
60
π
3
cm
3
B.
24
π
13
cm
3...
Đọc tiếp
Cho hình trụ (T)có bán kính bằng 4 cm mặt phẳng (P) cắt hai đáy của hình trụ theo hai dây AB và CD, AB = CD = 5 cm. Tứ giác ABCD là hình chữ nhật AD và BC không là đường sinh,góc giữa mp (P) và mặt phẳng chứa đáy của hình trụ bằng 60 ° . Thể tích của khối trụ là:
A. 60 π 3 cm 3
B. 24 π 13 cm 3
C. 16 π 13 cm 3
D. 48 π 13 cm 3
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất. A.
h
R
2
B.
h
R
C.
h
R
2
D.
h
R
2...
Đọc tiếp
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
A. h = R 2
B. h = R
C. h = R 2
D. h = R 2 2
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất. A.
h
R
2
.
B. h R C.
h
R
2
.
D.
h...
Đọc tiếp
Cho mặt cầu (S) có bán kính R. Một hình trụ có chiều cao h và bán kính đáy r thay đổi nội tiếp mặt cầu. Tính chiều cao h theo R sao cho diện tích xung quanh của hình trụ lớn nhất.
A. h = R 2 .
B. h = R
C. h = R 2 .
D. h = R 2 2 .
Cho một hình trụ có chiều cao và bán kính đều bằng a. Một hình vuông ABCD có hai cạnh AB, CD lần lượt là hai dây cung của hai đường tròn đáy, cạnh AD, BC không phải là đường sinh của hình trụ. Tính cạnh của hình vuông này A. a B. 2a C.
a
5
2
D.
a
10
2
Đọc tiếp
Cho một hình trụ có chiều cao và bán kính đều bằng a. Một hình vuông ABCD có hai cạnh AB, CD lần lượt là hai dây cung của hai đường tròn đáy, cạnh AD, BC không phải là đường sinh của hình trụ. Tính cạnh của hình vuông này
A. a
B. 2a
C. a 5 2
D. a 10 2