Các câu hỏi tương tự
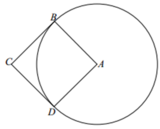
Trong mặt phẳng (P) cho hình vuông ABCD có cạnh bằng 5 và đường tròn (C) có tâm A, đường kính 10. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh trục là đường AC. A.
1000
π
+
375
π
2
6
B.
1000
π
+...
Đọc tiếp
Trong mặt phẳng (P) cho hình vuông ABCD có cạnh bằng 5 và đường tròn (C) có tâm A, đường kính 10. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh trục là đường AC.
A. 1000 π + 375 π 2 6
B. 1000 π + 375 π 2 6
C. 500 π + 125 π 2 6
D. 500 π + 375 π 2 6
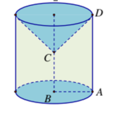
Cho hình thang ABCD vuông tại A và B với
A
B
B
C
A
D
2
a
.
Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành. A.
V
4
π
a
3...
Đọc tiếp
Cho hình thang ABCD vuông tại A và B với A B = B C = A D 2 = a . Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành.
A. V = 4 π a 3 3
B. V = 5 π a 3 3
C. V = π a 3
D. V = 7 π a 3 3
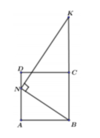
Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho
A
N
2
D
N
.
Đường thẳng qua N vuông góc với BN cắt BC tại K. Thể tích V của khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK là A.
V
7
6
π
a
3
B.
V
14
9
π
a
3...
Đọc tiếp
Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho A N = 2 D N . Đường thẳng qua N vuông góc với BN cắt BC tại K. Thể tích V của khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK là
A. V = 7 6 π a 3
B. V = 14 9 π a 3
C. V = 6 7 π a 3
D. V = 9 14 π a 3
Cho hình thang ABCD vuông A và B với
A
B
B
C
A
D
2
a
. Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành. A.
V
4
πa
3
3
B.
V...
Đọc tiếp
Cho hình thang ABCD vuông A và B với A B = B C = A D 2 = a . Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành.
A. V = 4 πa 3 3
B. V = 5 πa 3 3
C. V = 7 πa 3 3
D. V = πa 3
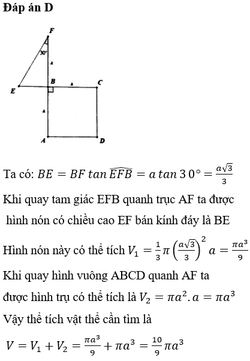
Cho hình chữ nhật ABCD có AB4,AD8 (như hình vẽ). Gọi M, N, E, F lần lượt là trung điểm BC, AD, BN và NC. Tính thể tích V của vật thể tròn xoay khi quay hình tứ giác BEFC quanh trục AB. A. 90
π
B. 96
π
C. 84
π
D. 100
π
Đọc tiếp
Cho hình chữ nhật ABCD có AB=4,AD=8 (như hình vẽ). Gọi M, N, E, F lần lượt là trung điểm BC, AD, BN và NC. Tính thể tích V của vật thể tròn xoay khi quay hình tứ giác BEFC quanh trục AB.
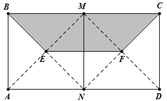
A. 90 π
B. 96 π
C. 84 π
D. 100 π
Cho tam giác vuông cân ABC có
A
B
A
C
a
2
và hình chữ nhật MNPQ với MQ 2MN được xếp chồng lên hình sao cho M, N lần lượt là trung điểm của AB và AC (như hình vẽ bên). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên xung quanh trục AI, với I là trung điểm của PQ. A.
V
11
π
a...
Đọc tiếp
Cho tam giác vuông cân ABC có A B = A C = a 2 và hình chữ nhật MNPQ với MQ = 2MN được xếp chồng lên hình sao cho M, N lần lượt là trung điểm của AB và AC (như hình vẽ bên). Tính thể tích V của vật thể tròn xoay khi quay mô hình trên xung quanh trục AI, với I là trung điểm của PQ.
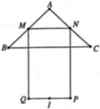
A. V = 11 π a 3 6
B. V = 5 π a 3 6
C. V = 11 π a 3 8
D. V = 17 π a 3 24
Gọi V là thể tích khối tròn xoay thành thành khi quay hình phẳng giới hạn bởi các đường
y
x
, y 0 và x 4 quanh trục Ox. Đường thẳng x a (0 a 4) cắt đồ thị hàm
y
x
tại M (hình vẽ bên). Gọi
V
1
là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng
V
2
V
1
. Khi đó: A. a...
Đọc tiếp
Gọi V là thể tích khối tròn xoay thành thành khi quay hình phẳng giới hạn bởi các đường y = x , y = 0 và x = 4 quanh trục Ox. Đường thẳng x = a (0 < a < 4) cắt đồ thị hàm y = x tại M (hình vẽ bên). Gọi V 1 là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng V = 2 V 1 . Khi đó:
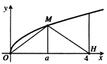
A. a = 2
B. a = 2 2
C. a = 5 2
D. a = 3
Trong không gian cho tam giác OIM vuông tại I,
I
O
M
^
30
∘
, IM a. Khi quay tam giác OIM quanh cạnh OI thì tạo thành một hình nón tròn xoay. Tính thể tích khối nón tròn xoay được tạo thành. A.
π
a
3
3...
Đọc tiếp
Trong không gian cho tam giác OIM vuông tại I, I O M ^ = 30 ∘ , IM = a. Khi quay tam giác OIM quanh cạnh OI thì tạo thành một hình nón tròn xoay. Tính thể tích khối nón tròn xoay được tạo thành.
A. π a 3 3
B. π a 3 3
C. 2 π a 3 3
D. 2 π a 3 3
Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là
V
1
. Tam giác ABC quay xung quanh trục d được khối tròn xoay có thể tích là
V
2
. Tính tỉ số
V
1
V
2
.
A.
2...
Đọc tiếp
Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là V 1 . Tam giác ABC quay xung
quanh trục d được khối tròn xoay có thể tích là V 2 . Tính tỉ số V 1 V 2 .
A. 2 3
B. 1 3
C. 3
D. 3 2