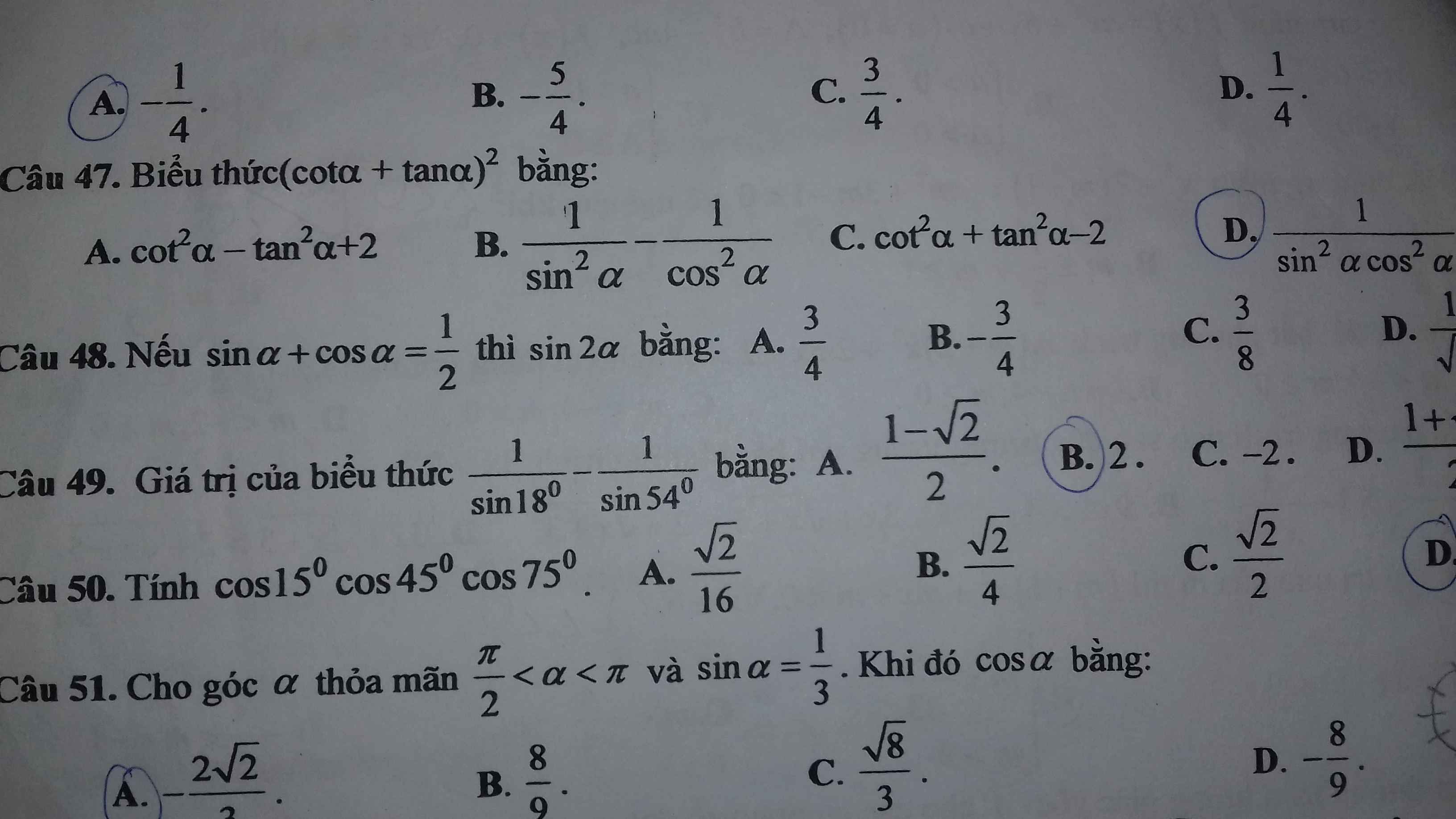47.
\(\left(cot\alpha+tan\alpha\right)^2=\left(\dfrac{cos\alpha}{sin\alpha}+\dfrac{sin\alpha}{cos\alpha}\right)^2=\left(\dfrac{cos^2\alpha+sin^2\alpha}{sin\alpha.cos\alpha}\right)^2=\dfrac{1}{sin^2\alpha.cos^2\alpha}\)
(cota +tana)\(^2\)=cot\(^2\)a+2cota.tana+tan\(^2\)a=(cot\(^2\)a +1)+(tan\(^2\)+1)=\(\dfrac{1}{sin^2a}\)+\(\dfrac{1}{cos^2a}\)=\(\dfrac{cos^2a+sin^2a}{cos^2a.sin^2a}\)=\(\dfrac{1}{cos^2a.sin^2a}\)
\((\cot\alpha+\tan\alpha)\)2 \(=\dfrac{\cos^2\alpha}{\sin^2\alpha}+\dfrac{\sin^2\alpha}{\cos^2\alpha}+2\dfrac{\cos}{\sin}\dfrac{\sin}{\cos}\)\(=\dfrac{\cos^4\alpha+\sin^4\alpha}{\sin^2\alpha.\cos^2\alpha}+2\)\(=\dfrac{\cos^4\alpha+\sin^4\alpha+2\sin^2\alpha.\cos^2\alpha}{\sin^2\alpha.\cos^2\alpha}\)\(=\dfrac{(\cos^2\alpha+\sin^2\alpha)^2}{\sin^2\alpha.\cos^2\alpha}\)
mà : \(\sin^2+\cos^2=1\)
\(\Rightarrow\)\((\cot\alpha+\tan\alpha)\)2\(=\)\(\dfrac{1}{\sin^2\alpha.\cos^2\alpha}\)
\(\Rightarrow\)Đáp án: D