`a)` Xét đường tròn `(O)`, có:
`BD` là dây cung, `BC` là đường kính.
Theo tính chất góc nội tiếp chắn nửa đường tròn, ta có: `hat{BDC} = 90°`.
Tương tự, `hat{BEC} = 90°`.
Suy ra:
`CD ⊥ AB` tại `D`.
`BE ⊥ AC` tại `E`.
`b)` Xét tứ giác `ADHE`, có:
`hat{ADH} = 90°` (`CD ⊥ AB`)
`hat{AEH} = 90°` (`BE ⊥ AC`)
`hat{DAE}` chung
`=>` Tứ giác `ADHE` nội tiếp (tứ giác có hai góc đối nhau bằng `180°`)
Gọi `F` là giao điểm của `AH` và `BC`.
Trong đường tròn ngoại tiếp tứ giác `ADHE`, ta có:
`hat{AHD} = hat{AED}` (cùng chắn cung `AD`)
Mà `hat{AED} = hat{ACB}` (cùng chắn cung `AB` trong đường tròn `(O)`)
`=> hat{AHD} = hat{ACB}`.
Xét `ΔAHD` và `ΔABC`, có:
`hat{AHD} = hat{ACB}` (cmt)
`hat{BAD}` chung
`=> ΔAHD ~ ΔABC` (g.g)
`=> hat{ADH} = hat{ABC}`.
Mà `hat{ADH} = 90°` (`CD ⊥ AB`)
`=> hat{ABC} = 90°`.
Vậy `AH ⊥ BC` tại `F`.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tam giác ABC nhọn nội tiếp (O), có AB<AC. Vẽ các đường cao BE, CF cắt nhau tại H
a. Chứng minh tứ giác BFEC nội tiếp
b. Chứng minh IE.IB=IF.IC
c. AO vuông góc với EF
(Giúp mình vẽ hình và giải bài với ạ, mình xin cảm ơn)
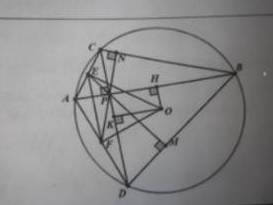
Mọi người có bài nào mà hình của nó trông như hình dưới này k? Cho mình xin với ạ, mình đg cần rất gấp
Có ai ko giúp em bài 7 với ạ. Em đang cần gấp trước 3h40 ạ .em xin cảm ơn ạ
Cho mik xin lời giải chi tiết vs ạ
Mọi người ơi cho mình hỏi: 1 bài hình 3,5 điểm mà mình vẽ sai hình thì trừ bao nhiêu điểm ạ? Bài đấy, hình với chứng minh không ảnh hưởng lắm: kiểu như vẽ hình sai nhưng chứng minh vẫn đúng á!
mn giúp mik vs ạ, phải đúng chuẩn và đủ nha ạ, bài hình thì phải có hình ạ


giúp mik bài 7 ạ
Gửi tất cả các bạn. Đăng bài lần sau nhớ có hình ko vẽ hình ra mệt lắm. Đăng luôn hình mik giải cho nhanh
Xin mọi người giúp dùm em bài này ạ. Em xin cám ơn
\(\sqrt{\frac{2}{8+3\sqrt{7}}}+\sqrt{\frac{38-14\sqrt{7}}{3-\sqrt{7}}}\)
Cho hình thang ABCD có góc A, D vuông. CD=2AB=2AD.
° Tính: tan của góc BDC, sin của góc BAC, cos của góc ACB.
Mình đã vẽ hình và nghĩ nhiều nhưng chưa làm được. Nhờ các bạn, các anh, các chị giúp đỡ ạ. Mình/em xin cảm ơn nhiều ạ.

















