\(+,\) Ta có:
\(\widehat{BAx}=180^0-70^0=110^0\)
\(AC\) là phân giác của \(\widehat{BAx}\)
nên : \(\widehat{BAC}=\widehat{CAx}=\dfrac{1}{2}\widehat{BAx}\)
\(\widehat{BAC}=\widehat{CAx}=\dfrac{1}{2}.110^0\)
\(\widehat{BAC}=\widehat{CAx}=55^0\)
\(+,\) \(\widehat{CAx}=\widehat{ACB}=55^0\)
Mà \(\widehat{CAx}\) và \(\widehat{ABC}\) so le trong
\(\rightarrow Ax\text{//}BC\)
Ta có:AC là p/g của BAx^
⇒BAC^=CAx^
Ta có:BAC^+CAx^+70°=180°
BAC^+CAx^=180°-70°=110°
mà BAC^=BAx^
⇒BAC^=CAx^=\(\dfrac{110\text{°}}{2}\)=55°
Ta thấyCAx^=ABC^=55°
mà 2 góc ở vị trí so le trong ⇒Ax//BC

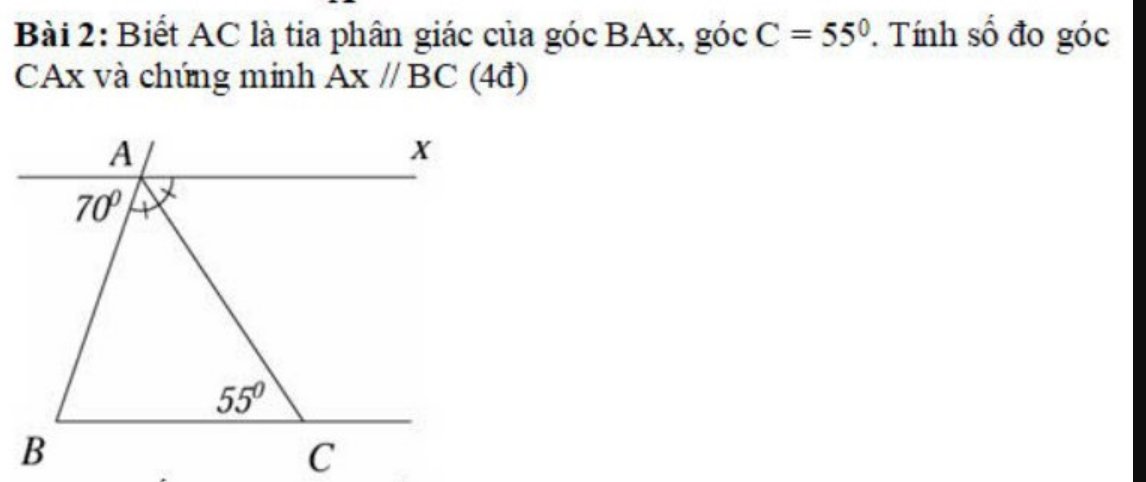














 Câu Này Có Sai Không Mọi Người ?
Câu Này Có Sai Không Mọi Người ?