\(S_{\left(S_1\right)}=4\pi R_1^2\)
\(S_{\left(S_2\right)}=4\pi R_2^2=4\pi\left(2R_1\right)^2=4.4\pi R_1^2\)
\(\Rightarrow\dfrac{S_{\left(S_2\right)}}{S_{\left(S_1\right)}}=4\)
Cho mặt cầu ( S 1 ) có bán kính R 1 , cho mặt cầu ( S 2 ) có bán kính R 2 = 2 R 1 . Tính tỉ số diện tích của mặt cầu ( S 2 ) và ( S 1 )
A. 1 2
B. 3
C. 4
D. 2
Cho mặt cầu ( S 1 ) có bán kính R 1 , mặt cầu S 2 có bán kính R 2 = 2 R 1 . Tính tỷ số diện tích của mặt cầu ( S 1 ) và ( S 2 ) ?
A. 4
B. 3
C. 1 2
D. 2
Cho tứ diện đều ABCD có mặt cầu nội tiếp là S 1 và mặt cầu ngoại tiếp là S 2 . Một hình lập phương ngoại tiếp S 2 và nội tiếp trong mặt cầu S 2 . Gọi r 1 , r 2 , r 3 lần lượt là bán kính các mặt cầu S 1 , S 2 , S 3 . Khẳng định nào sau đây đúng?
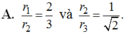
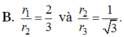
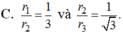
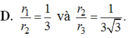
Cho hai mặt cầu ( S 1 ) có tâm I 1 , bán kính R 1 = 1 , ( S 2 ) có tâm I 2 bán kính R 2 = 5. Lần lượt lấy hai điểm M 1 , M 2 thuộc hai mặt cầu ( S 1 ) , ( S 2 ) . Gọi K là trung điểm M 1 M 2 . Khi M 1 M 2 di chuyển trên ( S 1 ) , ( S 2 ) thì K quét miền không gian là một khối tròn xoay có thể tích bằng?
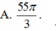
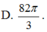
Cho hai mặt cầu ( S 1 ) v à ( S 2 ) đồng tâm I, có bán kính lần lượt là R 1 = 2 v à R 2 = 10 . Xét tứ diện ABCD có hai đỉnh A , B nằm trên ( S 1 ) và hai đỉnh C , D nằm trên ( S 2 ) . Thể tích lớn nhất của khối tứ diện ABCD bằng
Cho hai mặt cầu ( S 1 ) , S 2 có cùng bán kính R=3 thỏa mãn tính chất tâm của S 1 thuộc S 2 và ngược lại. Tính thể tích phần chung V của hai khối cầu tạo bởi S 1 , S 2 .
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;2;1), B(3;-1;1), C(-1;-1;1). Gọi S 1 là mặt cầu tâm A, bán kính bằng 2; S 2 và S 3 là hai mặt cầu có tâm lần lượt là B, C và bán kính đều bằng 1. Trong các mặt phẳng tiếp xúc với cả 3 mặt cầu S 1 , S 2 , S 3 có bao nhiêu mặt phẳng vuông góc với mặt phẳng (Oyz)?
A. 3
B. 1
C. 4
D. 2
Trong không gian Oxyz, cho mặt cầu (S1) có tâm I(2;1;1) có bán kính bằng 4 và mặt cầu (S2) có tâm J(2;1;5) có bán kính bằng 2. (P) là mặt phẳng thay đổi tiếp xúc với hai mặt cầu (S1) (S1) Đặt M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của khoảng cách từ điểm O đến (P). Giá trị M + m bằng?
A. 8 3
B. 9
C. 8
D. 15
Trong không gian Oxyz, cho ba điểm A(10;1;1), B(10;4;1) và C(10;1;5). Gọi S 1 là mặt cầu có tâm A, bán kính bằng 1; gọi S 2 là mặt cầu có tâm B, bán kính bằng 2 và S 3 là mặt cầu có tâm C, bán kính bằng 4. Hỏi có bao nhiêu mặt phẳng tiếp xúc với cả ba mặt cầu.
A.4.
B.7.
C.2.
D. 3.
