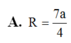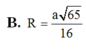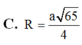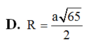\(S=4\pi R^2=36\pi\Rightarrow R=3\)
\(\Rightarrow OB=R=3\)
Áp dụng định lý Pitago cho tam giác OAB:
\(AB=\sqrt{OA^2-OB^2}=\sqrt{5^2-3^2}=4\)
\(S=4\pi R^2=36\pi\Rightarrow R=3\)
\(\Rightarrow OB=R=3\)
Áp dụng định lý Pitago cho tam giác OAB:
\(AB=\sqrt{OA^2-OB^2}=\sqrt{5^2-3^2}=4\)
Cho mặt cầu (S) có tâm O và bán kính R biết diện tích của (S) là 36π. Qua A kẻ 2 tiếp tuyến từ (S) có tiếp điểm lần lượt là M,N và góc MAN là 60°. Độ dài MN là
Cho mặt cầu (S) có tâm O và bán kính R biết diện tích của (S) là 36π. Hai điểm A,B thuộc (S) và khoảng cách từ O đến AB là 2 căn 2 Tính AB
cho mặt cầu (S) có tâm O và bán kính R. biết diện tích của (S) là 36π. thể tích của (S) là
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;0;-1) và mặt phẳng (P): x+y-z-3=0. Gọi (S) là mặt cầu có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng 17 2 . Tính bán kính R của mặt cầu (S).
A. R=3.
B. R=9
C. R=1
D. R=5.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu ( S ) : x - 1 2 + y - 1 2 + z 2 = 0 và một điểm M(2;3;1) Từ M kẻ được vô số các tiếp tuyến tới (S), biết tập hợp các tiếp điểm là đường tròn (C). Tính bán kính r của đường tròn (C).
A. r = 2 3 3
B. r = 3 3
C. r = 2 3
D. r = 3 2
Cho đường tròn tâm O có đường kính AB=2a nằm trong mặt phẳng (P). Gọi I là điểm đối xứng với O qua A. Lấy điểm S sao cho SI vuông góc với mặt phẳng (P) và SI=2a. Tính bán kính R của mặt cầu qua đường tròn tâm O và điểm S.
A. R = a 65 4
B. R = a 65 16
C. R = a 5
D. R = 7 a 4
Cho mặt cầu (S) tâm I bán kính R. M là điểm thỏa mãn I M = 3 R 2 . Hai mặt phẳng (P), (Q) qua M tiếp xúc với (S) lần lượt tại A và B. Biết góc giữa (P) và (Q) bằng 60°. Độ dài đoạn thẳng AB bằng:
A. AB=R
B. AB=R 3
C. AB= 3 R 2
D. AB=R hoặc AB=R 3
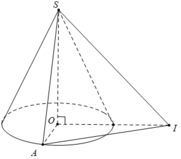
Cho hình nón đỉnh S với đáy là đường tròn tâm O bán kính R. Gọi I là một điểm nằm trên mặt phẳng đáy sao cho OI = R 3 . Giả sử A là điểm nằm trên đường tròn (O; R) sao cho OA ⊥ OI. Biết rằng tam giác SAI vuông cân tại S. Khi đó, diện tích xung quanh S xq của hình nón và thể tích V của khối nón là:
A. S xq = πR 2 ; V = πR 3 3
B. S xq = 2 πR 2 ; V = 2 πR 3 3
C. S xq = πR 2 2 2 ; V = πR 3 6
D. S xq = πR 2 ; V = 2 πR 3 3
Cho đường tròn tâm O có đường kính AB=2a nằm trong mặt phẳng (P). Gọi I là điểm đối xứng với O qua A. Lấy điểm S sao cho SI ⊥ (P) và SI=2a. Tính bán kính R mặt cầu đi qua đường tròn đã cho và điểm S.