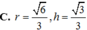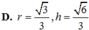\(\widehat{MON}=180^0-\widehat{MAN}=120^0\)
\(S=4\pi R^2=36\pi\Rightarrow R=3\Rightarrow OM=ON=3\)
Áp dụng định lý hàm cos cho tam giác MON:
\(MN=\sqrt{OM^2+ON^2-2OM.ON.cos\widehat{MON}}=\sqrt{3^2+3^2-2.3.3.cos120^0}=3\sqrt{3}\)
\(\widehat{MON}=180^0-\widehat{MAN}=120^0\)
\(S=4\pi R^2=36\pi\Rightarrow R=3\Rightarrow OM=ON=3\)
Áp dụng định lý hàm cos cho tam giác MON:
\(MN=\sqrt{OM^2+ON^2-2OM.ON.cos\widehat{MON}}=\sqrt{3^2+3^2-2.3.3.cos120^0}=3\sqrt{3}\)
Cho mặt cầu (S) có tâm O và bán kính R biết diện tích của (S) là 36π. Điểm A nằm ngoài (S) sao cho OA=5. Tiếp tuyến kẻ từ A tới (S) có tiếp điểm là B. Độ dài AB là
Cho mặt cầu (S) có tâm O và bán kính R biết diện tích của (S) là 36π. Hai điểm A,B thuộc (S) và khoảng cách từ O đến AB là 2 căn 2 Tính AB
Cho mặt cầu (S) tâm I bán kính R. M là điểm thỏa mãn I M = 3 R 2 . Hai mặt phẳng (P), (Q) qua M tiếp xúc với (S) lần lượt tại A và B. Biết góc giữa (P) và (Q) bằng 60°. Độ dài đoạn thẳng AB bằng:
A. AB=R
B. AB=R 3
C. AB= 3 R 2
D. AB=R hoặc AB=R 3
cho mặt cầu (S) có tâm O và bán kính R. biết diện tích của (S) là 36π. thể tích của (S) là
Cho mặt cầu (S) tâm I bán kính R . M là điểm thỏa mãn IM = 3 R 2 . Hai mặt phẳng (P),(Q) qua M và tiếp xúc với (S) lần lượt tại A và B. Biết góc giữa (P) và (Q) bằng 60 ∘ . Độ dài đoạn thẳng AB bằng:
![]()
![]()
![]()
![]()
Cho mặt cầu (S) tâm I bán kính R. M là điểm thỏa mãn I M = 3 R 2 . Hai mặt phẳng (P), (Q) qua M và tiếp xúc với (S) lần lượt tại A và B. Biết góc giữa (P) và (Q) bằng 60 o . Độ dài đoạn thẳng AB bằng:
A. AB=R
B. AB=R 3
C . A B = 3 R 2
D . A B = R h o ặ c A B = R 3
Trong không gian với hệ trục tọa độ Oxyz, cho các mặt cầu (S1), (S2), (S3) có bán kính r=1 và lần lượt có tâm là các điểm A(0;3;-1), B(-2;1;-1), C(4;-1;-1). Gọi (S) là mặt cầu tiếp xúc với cả ba mặt cầu trên. Mặt cầu (S) có bán kính nhỏ nhất là
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho các mặt cầu ( S 1 ) , ( S 2 ) , ( S 3 ) có bán kính r=1 và lần lượt có tâm là các điểm A(0;3;-1), B(-2;1;-1), C(4;-1;-1). Gọi (S) là mặt cầu tiếp xúc với cả ba mặt cầu trên. Mặt cầu (S) có bán kính nhỏ nhất là bao nhiêu?
A. R= 10
B. R= 10 - 1
C. R= 2 2 - 1
D. 2 2
Khi cắt mặt cầu S (O, R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O, R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R = 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S (O, R) để khối trụ có thể tích lớn nhất.
![]()
![]()