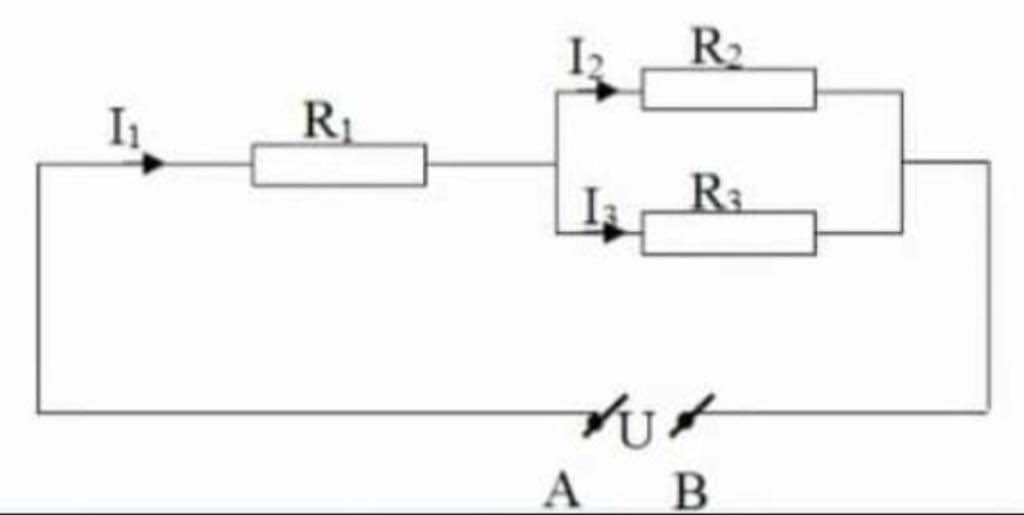
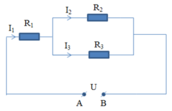
`(R_1 //// R_2)nt R_3`
`R_[tđ]=[U_[AB]]/I=60/4=15(\Omega)`
`@R_[tđ]=R_3+[R_1.R_2]/[R_1+R_2]`
`<=>15=8+[3R_2 ^2]/[4R_2]`
`<=>R_2=28/3(\Omega)=>R_1=3. 28/3=28(\Omega)`
`I=I_[12]=4(A)`
`=>U_[12]=I_[12].R_[12]=4.[28 .28/3]/[28+28/3]=28(V)=U_1=U_2`
`@I_1=[U_1]/[R_1]=28/28=1(A)`
`@I_2=[U_2]/[R_2]=28/[28/3]=3(A)`
\(MCD:\left(R_1//R_2\right)ntR_3\)
\(\rightarrow R_{td}=\dfrac{U}{I}=\dfrac{60}{4}=15\Omega\)
Ta có: \(R_{td}=\dfrac{R_1\cdot R_2}{R_1+R_2}+R_3=\dfrac{3R_2\cdot R_2}{3R_2+R_2}+8=\dfrac{3R_2^2}{4R_2}+8=\dfrac{3R_2}{4}+8\)
\(\rightarrow R_2=\dfrac{28}{3}\Omega\)
\(\rightarrow R_1=3R_2=3\cdot\dfrac{28}{3}=28\Omega\)
\(\rightarrow I=I_{12}=I_3=4A\)
\(\rightarrow U_{12}=U_1=U_2=I_{12}\cdot R_{12}=4\cdot\left(15-8\right)=28V\)
\(\rightarrow\left\{{}\begin{matrix}I_1=\dfrac{U_1}{R_1}=\dfrac{28}{28}=1A\\I_2=\dfrac{U_2}{R_2}=\dfrac{28}{\dfrac{28}{3}}=3A\end{matrix}\right.\)