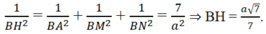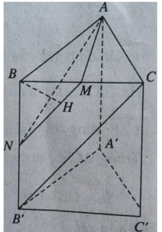
Gọi N là trung điểm của BB’, ta có: CB’ // MN nên CB’ // (AMN). Như vậy
d(BC’, AM) = d(B’, (AMN)) = d(B, (AMN))
(vì B, B’ đối xứng qua N ∈ (AMN)).
Hạ BH ⊥ (AMN), ta có d(B, (AMN)) = BH.
Nhận xét:
Tứ diện B.AMN có ba cạnh BA, BM, BN vuông góc nhau từng đôi một nên
Cho lăng trụ đứng tam giác ABC.A'B'C' có đáy là một tam giác vuông cân tại B, AB = BC = a, AA' = a 2 , M là trung điểm BC. Tính khoảng cách giữa hai đường thẳng AM và B'C
A . a 7
B . a 3 2
C . 2 a 5
D . a 3
Cho hình lăng trụ đứng ABC. A’B’C’ có đáy là ABC là tam giác vuông BA = BC =a, cạnh bên A A ' = a 2 .Gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM, B’C’.
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông BA = BC = a, cạnh bên AA' = a 2 . M là trung điểm của BC. Khoảng cách giữa AM và B'C là:
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông, BA=BC=a, cạnh bên A A ' = a 2 , M là trung điểm của BC. Khoảng cách giữa hai đường thẳng AM và B’C bằng
A. a 2 2
B. a 3 3
C. a 5 5
D. a 7 7
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông ở A, AB=2a AC=a, AA'=4a M là điểm thuộc cạnh AA' sao cho MA'=3MA . Tính khoảng cách giữa hai đường chéo nhau BC và C'M
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB = a, AC = a 3 Hình chiếu vuông góc của A' lên mặt phẳng (ABC) là trung điểm H của BC, HA' = a 5 Gọi φ là góc giữa hai đường thẳng A'B và B'C.
Tính cos φ
A.cos φ = 7 3 48
B. cos φ = 3 2
C. cos φ = 1 2
D. cos φ = 7 3 24
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB=a, AC =a 3 và BB'C'C là hình vuông. Khoảng cách giữa hai đường thẳng AA' và BC' là
A. a 3 2
B. 3 a 2 4
C. a
D. a 3
Cho hình lăng trụ đứng ABC.A’B’C’có đáy là tam giác vuông và AB=BC=a, AA'= a 2 . Gọi M là trung điểm của BC. Tính khoảng cách d của hai đường thẳng AM và B’C
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Biết thể tích của khối lăng trụ là a 3 3 4 . Tính khoảng cách giữa hai đường thẳng AA' và BC
A. 4 a 3
B. 2 a 3
C. 3 a 4
D. 3 a 2
