Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có ABa;AD2a và AA3a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ACB’D’. A.
a
3
2
B.
a
14
2
C.
a
6
2
D.
a
3...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=a;AD=2a và AA'=3a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ACB’D’.
A. a 3 2
B. a 14 2
C. a 6 2
D. a 3 4
Cho tứ diện ABCD có (ACD) vuông (BCD), tam giác ACD đều cạnh 2a, tam giác BCD cân tại B có BC=acan5. Tìm tâm bán kính mặt cầu ngoại tiếp
p/s ve hình hộ mk vs
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C với CACBa;SAa
3
; SBa
5
và SCa
2
. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC? A.
a
11
6
B.
a
11
2
C.
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C với CA=CB=a;SA=a 3 ; SB=a 5 và SC=a 2 . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC?
A. a 11 6
B. a 11 2
C. a 11 3
D. a 11 4
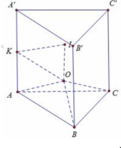
Cho lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác vuông cân tại A. E là trung điểm của B’C’, CB’ cắt BE tại M. Tính thể tích V của khối tứ diện ABCM biết AB 3a, AA’ 6a. A.
V
7
a
3
.
B.
V
6
2
a
3
.
C.
V
8
a...
Đọc tiếp
Cho lăng trụ đứng ABC.A’B’C’, đáy ABC là tam giác vuông cân tại A. E là trung điểm của B’C’, CB’ cắt BE tại M. Tính thể tích V của khối tứ diện ABCM biết AB = 3a, AA’ = 6a.
A. V = 7 a 3 .
B. V = 6 2 a 3 .
C. V = 8 a 3 .
D. V = 6 a 3 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
2
2
, cạnh bên SA vuông góc với mặt phẳng đáy và SA3 Mặt phẳng
α
qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tự diện CMNP. A.
V
64
2
π
3
B.
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy và SA=3 Mặt phẳng α qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tự diện CMNP.
A. V = 64 2 π 3
B. V = 125 π 6
C. V = 32 π 3
D. V = 10 Sπ 3
Cho hình chóp đều n cạnh
n
≥
3
. Cho biết bán kính đường tròn ngoại tiếp đa giác đáy là R và góc giữa mặt bên và mặt đáy bằng
60
°
, thể tích khối chóp bằng
3
3
4
.
R
3
. Tìm n? A.
n
4...
Đọc tiếp
Cho hình chóp đều n cạnh n ≥ 3 . Cho biết bán kính đường tròn ngoại tiếp đa giác đáy là R và góc giữa mặt bên và mặt đáy bằng 60 ° , thể tích khối chóp bằng 3 3 4 . R 3 . Tìm n?
A. n = 4
B. n = 8
C. n = 10
D. n = 6
Cho tứ diện ABCD đều có cạnh bằng a và trọng tâm G. Tập hợp các điểm M thỏa mãn
M
A
2
+
M
B
2
+
M
C
2
+
M
D
2
11
a
2
2
là mặt cầu. A.
S
G...
Đọc tiếp
Cho tứ diện ABCD đều có cạnh bằng a và trọng tâm G. Tập hợp các điểm M thỏa mãn M A 2 + M B 2 + M C 2 + M D 2 = 11 a 2 2 là mặt cầu.
A. S G ; a
B. S G ; 2 a
C. S B ; a
D. S C ; 2 a
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng
(
α
)
:
x
1
,
(
β
)
:
y
-
1
,
(
γ
)
:
z
1
. Bán kính của mặt cầu (S) bằng A.
33
B. 1 C.
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) đi qua điểm A(2;-2;5) và tiếp xúc với các mặt phẳng ( α ) : x = 1 , ( β ) : y = - 1 , ( γ ) : z = 1 . Bán kính của mặt cầu (S) bằng
A. 33
B. 1
C. 3 2
D. 3
Trong không gian với hệ tọa độ Oxyz, xét mặt cầu (S) đi qua hai điểm A(1;2;1); B(3;2;3) , có tâm thuộc mặt phẳng (P):x-y-3=0, đồng thời có bán kính nhỏ nhất, hãy tính bán kính R thuộc mặt cầu (S)?
A. 1
B. 2
C. 2
D. 2 2