Các câu hỏi tương tự
Cho lăng trụ ABCD. ABCD có đáy ABCD là hình chữ nhật, AB3, AD
a
3
. Hình chiếu vuông góc của điểm A trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B đến mặt phẳng (ABD) A.
a
3
3
B.
a
...
Đọc tiếp
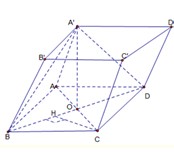
Cho lăng trụ ABCD. A'B'C'D' có đáy ABCD là hình chữ nhật, AB=3, AD= a 3 . Hình chiếu vuông góc của điểm A' trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B' đến mặt phẳng (A'BD)
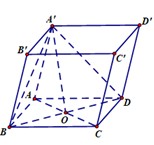
A. a 3 3
B. a 3 6
C. a 3 2
D. a 3 4
Cho lăng trụ
A
B
C
D
.
A
B
C
D
có đáy ABCD là hình chữ nhật với
A
B
a
,
A
D
a
3
.
Hình chiếu vuông góc của A lên
A
B
C
D
trùng với giao điểm của AC và B...
Đọc tiếp
Cho lăng trụ A B C D . A ' B ' C ' D ' có đáy ABCD là hình chữ nhật với A B = a , A D = a 3 . Hình chiếu vuông góc của A' lên A B C D trùng với giao điểm của AC và BD. Tính khoảng cách từ điểm B' đến mặt phẳng A ' B D .
A. a 3
B. a 2
C. a 3 2
D. a 3 6
Cho lăng trụ ABCD. ABCD có đáy ABCD là hình chữ nhật với ABa,
A
D
a
3
. Hình chiếu vuông góc của A lên (ABCD) trùng với giao điểm của AC và BD. Tính khoảng cách từ điểm B đến mặt phẳng (ABD) A.
a
3
B.
a
2
C.
a
3
2
D.
a...
Đọc tiếp
Cho lăng trụ ABCD. A'B'C'D' có đáy ABCD là hình chữ nhật với AB=a, A D = a 3 . Hình chiếu vuông góc của A' lên (ABCD) trùng với giao điểm của AC và BD. Tính khoảng cách từ điểm B' đến mặt phẳng (A'BD)
A. a 3
B. a 2
C. a 3 2
D. a 3 6
Cho lăng trụ ABCD. ABCD có đáy ABCD là hình chữ nhật, ABa,
A
D
a
3
. Hình chiếu vuông góc của điểm A trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B đến mặt phẳng (ABD) A.
a
3
3
B.
a
3
6
C.
a...
Đọc tiếp
Cho lăng trụ ABCD. A'B'C'D' có đáy ABCD là hình chữ nhật, AB=a, A D = a 3 . Hình chiếu vuông góc của điểm A' trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B' đến mặt phẳng (A'BD)
A. a 3 3
B. a 3 6
C. a 3 2
D. a 3 4
Cho lăng trụ
A
B
C
D
.
A
B
C
D
có đáy ABCD là hình chữ nhật
A
B
a
,
A
D
a
3
.
Hình chiếu vuông góc của điểm A¢ trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B¢ đến mặt phẳng (A’BD) là A.
a
3
3
B. ...
Đọc tiếp
Cho lăng trụ A B C D . A ' B ' C ' D ' có đáy ABCD là hình chữ nhật A B = a , A D = a 3 . Hình
chiếu vuông góc của điểm A¢ trên mặt phẳng (ABCD) trùng với giao điểm AC và BD. Tính khoảng cách từ điểm B¢ đến mặt phẳng (A’BD) là
A. a 3 3
B. a 3 4
C. a 3 2
D. a 3 6
Cho lăng trụ
A
B
C
D
.
A
1
B
1
C
1
D
1
có đáy ABCD là hình chữ nhật với
A
B
a
,
A
D
a
3
.
Hình chiếu vuông góc của
A
1
lên ( ABCD) trung với giao điểm của A...
Đọc tiếp
Cho lăng trụ A B C D . A 1 B 1 C 1 D 1 có đáy ABCD là hình chữ nhật với A B = a , A D = a 3 . Hình chiếu vuông góc của A 1 lên ( ABCD) trung với giao điểm của AC và BD. Tính khoảng cách từ điểm B1 đến mặt phẳng ( A 1 B D )
A. a 3
B. a 2
C. a 3 2
D. a 3 6
Cho hình hộp ABCD.ABCD có đáy ABCD là hình thoi cạnh a,
BCD
120°
và
AA
5
a
2
.
Hình chiếu vuông góc của A lên mặt phẳng ABCD trùng với giao điểm của AC và BD. Tính theo a thể thích khối hộp ABCD.ABCD: A.
V
2...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, BCD =120° và AA ' = 5 a 2 . Hình chiếu vuông góc của A' lên mặt phẳng ABCD trùng với giao điểm của AC và BD. Tính theo a thể thích khối hộp ABCD.A'B'C'D':
A. V = 2 2 a 2
B. V = 2 2 a 3
C. V = 6 2 a 3
D. V = 3 2 2 a 3
Cho hình hộp ABCD.ABCD có đáy ABCD là hình thoi canh a,
B
C
D
^
120
o
và AA
7
a
2
. Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.ACBCD A.
V
12
a
3...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi canh a, B C D ^ = 120 o và AA' = 7 a 2 . Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A'CB'C'D'
A. V = 12 a 3
B. V = 3 a 3
C. V = 9 a 3
D. V = 6 a 3
Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D, ABADa, CD2a. Hình chiếu của S lên mặt phẳng (ABCD) trùng với trung điểm của BD Biết thể tích tứ diện SBCD bằng
a
3
6
. Tính khoảng cách từ A đến mặt phẳng (SBC) là: A.
a
3
2
B.
a
2...
Đọc tiếp
Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D, AB=AD=a, CD=2a. Hình chiếu của S lên mặt phẳng (ABCD) trùng với trung điểm của BD Biết thể tích tứ diện SBCD bằng a 3 6 . Tính khoảng cách từ A đến mặt phẳng (SBC) là:
A. a 3 2
B. a 2 6
C. a 3 6
D. a 6 4