Các câu hỏi tương tự
Cho lăng trụ ABCD.ABCD có đáy ABCD là hình chữ nhật với
A
B
a
,
A
D
a
3
. Hình chiếu vuông góc của A lên (ABCD) trùng với giao điểm của AC và BD. Tính khoảng cách từ điểm B đến mặt phẳng (ABD) A.
a
3...
Đọc tiếp
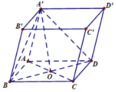
Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật với A B = a , A D = a 3 . Hình chiếu vuông góc của A' lên (ABCD) trùng với giao điểm của AC và BD. Tính khoảng cách từ điểm B' đến mặt phẳng (A'BD)
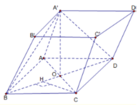
A. a 3
B. a 2
C. a 3 2
D. a 3 6
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a
3
, BD3a. Hình chiếu vuông góc của B trên mặt phẳng (ABCD) trùng với trung điểm A’C’. Gọi
α
là góc giữa 2 mặt phẳng (ABCD) và (CDDC). Thể tích của khối hộp ABCD.ABCD bằng
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a 3 , BD=3a. Hình chiếu vuông góc của B trên mặt phẳng (A'B'C'D') trùng với trung điểm A’C’. Gọi α là góc giữa 2 mặt phẳng (ABCD) và (CDD'C'). Thể tích của khối hộp ABCD.A'B'C'D' bằng
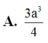
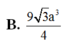
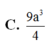
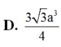
Cho hình hộp ABCD.ABCD có đáy ABCD là hình thoi cạnh a, góc BCD
120
o
và AA Hình chiếu vuông góc của A lên mặt phẳng ABCD trùng với giao điểm của AC và BD. Tính theo a thể thích khối hộp ABCD.ABCD
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, góc BCD= 120 o và AA'= Hình chiếu vuông góc của A' lên mặt phẳng ABCD trùng với giao điểm của AC và BD.
Tính theo a thể thích khối hộp ABCD.A'B'C'D'

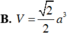
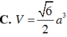
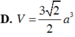
Cho hình hộp ABCD.ABCD có đáy ABCD là hình thoi cạnh a,
B
C
D
⏜
120
∘
và AA
7
a
2
. Hình chiếu vuông góc của A lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.ABCD A. V 12
a
3
B....
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, B C D ⏜ = 120 ∘ và AA' = 7 a 2 . Hình chiếu vuông góc của A' lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A'B'C'D'
A. V = 12 a 3
B. V = 3 a 3
C. V = 9 a 3
D. V = 6 a 3
Cho hình hộp ABCD.ABCD có đáy ABCD là hình thoi cạnh a,
B
C
D
^
120
°
và AA
7
α
2
Hình chiếu vuông góc của A lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.ABCD
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, B C D ^ =120 ° và AA'= 7 α 2 Hình chiếu vuông góc của A' lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A'B'C'D'
![]()
![]()
![]()
![]()
Cho hình hộp ABCD.ABCD có đáy là hình chữ nhật, hình chiếu của A lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB a, AD 2a và thể tích hình hộp đã cho bằng 2
a
3
. Khoảng cách từ B đến mặt phẳng (ADCB) bằng:A.
2
a
6
B.
2...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, hình chiếu của A' lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB = a, AD = 2a và thể tích hình hộp đã cho bằng 2 a 3 . Khoảng cách từ B đến mặt phẳng (A'DCB') bằng:
A. 2 a 6 B. 2 a 3
C. 3 a 3 D. a 2
Cho lăng trụ
A
B
C
D
.
A
B
C
D
có đáy là hình vuông cạnh
a
3
. Hình chiếu vuông góc của điểm A lên mặt phẳng
(
A
B
C
D
)
trùng với tâm O của hình vuông
A
B
C
D
. Biết rằng...
Đọc tiếp
Cho lăng trụ A B C D . A ' B ' C ' D ' có đáy là hình vuông cạnh a 3 . Hình chiếu vuông góc của điểm A lên mặt phẳng ( A ' B ' C ' D ' ) trùng với tâm O của hình vuông A ' B ' C ' D ' . Biết rằng khoảng cách từ trọng tâm G của tam giác AB’D’ đến mặt phẳng (AA’D) bằng a 2 . Khoảng cách từ điểm O đến mặt phẳng ( A D C ' B ' ) bằng
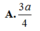

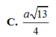
![]()
: Cho hình chóp sabcd có đáy ABCD là hình chữ nhật, ab=a, bc=a căn 3, sa vuông góc với (abcd) Góc giữa SC và mặt đáy bằng 45. Khoảng cách từ điểm A đến mặt phẳng (scd) bằng
Cho hình hộp ABCD.ABCD có đáy ABCD là hình thoi cạnh a,
B
C
D
^
120
∘
và AA
7
a
2
Hình chiếu vuông góc của A lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD.Tính theo a thể tích khối hộp ABCD.ABCD
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, B C D ^ = 120 ∘ và AA' = 7 a 2 Hình chiếu vuông góc của A' lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD.Tính theo a thể tích khối hộp ABCD.A'B'C'D'
![]()
![]()
![]()
![]()