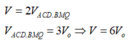Các câu hỏi tương tự
Cho khối tứ diện ABCD có thể tích
V
0
Dựng hình hộp sao cho AB, AC, AD là ba cạnh của hình hộp. Tính thể tích V của khối hộp đó. A.
V
2
V
0
B.
V
6
V
0
C.
V
3
V...
Đọc tiếp
Cho khối tứ diện ABCD có thể tích V 0 Dựng hình hộp sao cho AB, AC, AD là ba cạnh của hình hộp. Tính thể tích V của khối hộp đó.
A. V = 2 V 0
B. V = 6 V 0
C. V = 3 V 0
D. V = 4 V 0
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng
A
B
a
,
A
C
a
2
,
A
D
a
3
,
a
0
.
Thể tích V của khối tứ diện ABCD là: A.
V
1
3
a
3...
Đọc tiếp
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng A B = a , A C = a 2 , A D = a 3 , a > 0 . Thể tích V của khối tứ diện ABCD là:
A. V = 1 3 a 3 6
B. V = 1 6 a 3 6
C. V = 1 2 a 3 6
D. V = 1 9 a 3 6
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có
A
B
a
,
A
A
2
a
.
Biết thể tích hình cầu ngoại tiếp tứ diện ABCD′ là
9
π
2
a
3
. Tính thể tích V của hình chữ nhật ABCD.A′B′C′D′. A.
4
a
3
B. ...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có A B = a , A A ' = 2 a . Biết thể tích hình cầu ngoại tiếp tứ diện ABCD′ là 9 π 2 a 3 . Tính thể tích V của hình chữ nhật ABCD.A′B′C′D′.
A. 4 a 3
B. 4 a 3 3
C. 2 a 3
D. 2 a 3 3
Cho hình hộp chữ nhật ABCD.ABCD có AB a, AA 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD là
9
πa
3
2
. Tính thể tích V của hình hộp chữ nhật ABCD.ABCD. A.
V
9
a
3
4
B.
V
4
a
3
C. ...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AA' = 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 πa 3 2 . Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
A. V = 9 a 3 4
B. V = 4 a 3
C. V = 4 a 3 3
D. V = 2 a 3
Cho hình hộp chữ nhật ABCD.ABCD có
A
D
2
a
,
A
C
2
3
a
. Tính theo a thể tích V của khối hộp ABCD.ABCD A.
V
2
6
a
3
B.
V
2
6...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có A D = 2 a , A C ' = 2 3 a . Tính theo a thể tích V của khối hộp ABCD.A'B'C'D'
A. V = 2 6 a 3
B. V = 2 6 a 3 3
C. V = 3 2 a 3
D. V = 6 a 3
Cho biết thể tích của một khối hộp chữ nhật là V, đáy là hình vuông cạnh a. Khi đó diện tích toàn phần của hình hộp bằng A.
S
t
p
2
2
V
a...
Đọc tiếp
Cho biết thể tích của một khối hộp chữ nhật là V, đáy là hình vuông cạnh a. Khi đó diện tích toàn phần của hình hộp bằng
A. S t p = 2 2 V a + a 2
B. S t p = 2 V a + a 2
C. S t p = 2 V a 2 + a
D. S t p = 4 V a 2 + a
Cho hình hộp đứng
A
B
C
D
.
A
B
C
D
có đáy ABCD là hình thoi có hai đường chéo
A
C
a
B
D
a
3
và cạnh bên
A
A
a
2
. Thể tích V của khối hộp đã cho là A.
V...
Đọc tiếp
Cho hình hộp đứng A B C D . A ' B ' C ' D ' có đáy ABCD là hình thoi có hai đường chéo A C = a B D = a 3 và cạnh bên A A ' = a 2 . Thể tích V của khối hộp đã cho là
A. V = 6 a 3
B. V = 6 6 a 3
C. V = 6 2 a 3
D. V = 6 4 a 3
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có ABa, ADb, AA’c. Tính thể tích V của khối chóp A.A’B’C’D’ A.
V
1
6
a
b
c
B.
V
a
b
c
C.
V
1
3
a
b
c
D.
V
1
2
a
b
c
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=a, AD=b, AA’=c. Tính thể tích V của khối chóp A.A’B’C’D’
A. V = 1 6 a b c
B. V = a b c
C. V = 1 3 a b c
D. V = 1 2 a b c
Cho hình hộp đứng ABCDA’B’C’D’ có đáy là hình vuông cạnh a, AC’ tạo với mặt bên (BCC’B’) với góc 30
°
. Tính thể tích V của khối hộp ABCDA’B’C’D’ A.
V
2
a
3
B.
V
2
a
3
C.
V
2
2
a
3
D.
V...
Đọc tiếp
Cho hình hộp đứng ABCDA’B’C’D’ có đáy là hình vuông cạnh a, AC’ tạo với mặt bên (BCC’B’) với góc 30 ° . Tính thể tích V của khối hộp ABCDA’B’C’D’
A. V = 2 a 3
B. V = 2 a 3
C. V = 2 2 a 3
D. V = 2 2 a 3