Ta có: VABC.A′B′C′=VBAA′C′C+VB.A′B′C′𝑉𝐴𝐵𝐶.𝐴′𝐵′𝐶′=𝑉𝐵𝐴𝐴′𝐶′𝐶+𝑉𝐵.𝐴′𝐵′𝐶′.
VBAA′C′C=VABC.A′B′C′−VB.A′B′C′=VABC.A′B′C′−13VABC.A′B′C′=23VABC.A′B′C′=2V3𝑉𝐵𝐴𝐴′𝐶′𝐶=𝑉𝐴𝐵𝐶.𝐴′𝐵′𝐶′−𝑉𝐵.𝐴′𝐵′𝐶′=𝑉𝐴𝐵𝐶.𝐴′𝐵′𝐶′−13𝑉𝐴𝐵𝐶.𝐴′𝐵′𝐶′=23𝑉𝐴𝐵𝐶.𝐴′𝐵′𝐶′=2𝑉3.
ko bt có đúng ko nữa ?
Ta có: VABC.A′B′C′=VBAA′C′C+VB.A′B′C′𝑉𝐴𝐵𝐶.𝐴′𝐵′𝐶′=𝑉𝐵𝐴𝐴′𝐶′𝐶+𝑉𝐵.𝐴′𝐵′𝐶′.
VBAA′C′C=VABC.A′B′C′−VB.A′B′C′=VABC.A′B′C′−13VABC.A′B′C′=23VABC.A′B′C′=2V3𝑉𝐵𝐴𝐴′𝐶′𝐶=𝑉𝐴𝐵𝐶.𝐴′𝐵′𝐶′−𝑉𝐵.𝐴′𝐵′𝐶′=𝑉𝐴𝐵𝐶.𝐴′𝐵′𝐶′−13𝑉𝐴𝐵𝐶.𝐴′𝐵′𝐶′=23𝑉𝐴𝐵𝐶.𝐴′𝐵′𝐶′=2𝑉3.
ko bt có đúng ko nữa ?
Cho khối lăng trụ ABC.A'B'C' . Gọi M là trung điểm của BB' , N là điểm trên cạnh CC' sao cho CN = NC’. Mặt phẳng ( AMN ) chia khối lăng trụ thành hai phần có thể tích V 1 và V 2 như hình vẽ. Tính tỉ số V 1 V 2
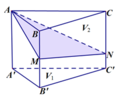
A. V 1 V 2 = 5 3
B. V 1 V 2 = 3 2
C. V 1 V 2 = 4 3
D. V 1 V 2 = 7 5
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M,N lần lượt là trung điểm của BB', CC'. Mặt phẳng (A'MN) chia khối lăng trụ thành hai phần, V 1 là thể tích của phần đa diện chứa điểm B, V 2 thể tích phần đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 2
B. V 1 V 2 = 2
C. V 1 V 2 = 3
D. V 1 V 2 = 5 2
Cho lăng trụ ABC.A'B'C', trên cạnh AA'', BB' lấy các điểm M, N sao cho AA' = 3A'M; BB' = 3B'N. Mặt phẳng (C'MN) chia khối lăng trụ đã cho thành hai phần. Gọi V 1 là thể tích khối chóp C'.A'B'NM, V 2 là thể tích khối đa diện ABC.MNC'. Tính tỉ số V 1 V 2
A . 2 9
B . 3 4
C . 2 7
D . 5 7
Cho lăng trụ ABC.A'B'C' trên các cạnh AA’, BB’ lấy các điểm M, N sao cho AA' = 3A'M, BB' = 3B'N. Mặt phẳng (C'MN) chia khối lăng trụ đã cho thành hai phần. Gọi V 1 là thể tích của khối chóp C'.A'B'MN, V 2 là thể tích của khối đa diện ABCMNC'. Tỉ số V 1 V 2 bằng:
A. V 1 V 2 = 4 7
B. V 1 V 2 = 2 7
C. V 1 V 2 = 1 7
D. V 1 V 2 = 3 7
Cho khối lăng trụ ABCD.A’B’C’D’ có thể tích bằng 36 c m 3 Gọi M là điểm bất kì thuộc mặt phẳng (ABCD). Tính thể tích V của khối chóp M.A’B’C’D’
![]()
![]()
![]()
![]()
Cho hình lăng trụ ABC.A'B'C' có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, A'C’, BB’. Thể tích của khối tứ diện CMNP bằng
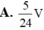
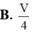
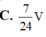
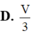
Cho hình lăng trụ ABC.A'B'C'. Gọi E, F lần lượt là trung điểm của BB' và CC'. Mặt phẳng (AEF) chia khối lăng trụ thành hai phần có thể tích V 1 và V 2 như hình vẽ. Tỉ số V 1 V 2 là
A. 1
B. 1 3
C. 1 4
D. 1 2
Cho hình lăng trụ ABC.A'B'C' Gọi E, F lần lượt là trung điểm của BB¢ và CC¢. Mặt phẳng (AEF) chia khối lăng trụ thành hai phần có thể tích V 1 và V 2 như hình vẽ.
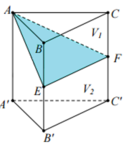
Tỉ số V 1 V 2 là
A. 1 2
B. 1
C. 1 3
D. 1 4
Cho khối lăng trụ tam giác ABC.A'B'C' có thể tích là V. Gọi I, J lần lượt là trung điểm của hai cạnh AA' và BB'. Khi đó thể tích của khối đa diện ABCIJC' bằng

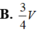
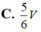
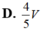
Cho lăng trụ tam giác ABC.A’B’C’ có thể tích là V. Gọi M, N là trung điểm của AB và CC'. Thể tích khối tứ diện B’MCN tính theo V là:
A. V 2
B. V 4
C. V 3
D. V 12