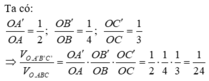Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm M(2,3,5) cắt các tia Ox, Oy, Oz lần lượt tại ba điểm A, B, C sao cho OA, OB, OC theo thứ tự lập thành cấp số nhân có công bội bằng 3. Khoảng cách từ O đến mặt phẳng (P) là A.
16
91
B.
24
91
C.
32
91
D. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm M(2,3,5) cắt các tia Ox, Oy, Oz lần lượt tại ba điểm A, B, C sao cho OA, OB, OC theo thứ tự lập thành cấp số nhân có công bội bằng 3. Khoảng cách từ O đến mặt phẳng (P) là
A. 16 91
B. 24 91
C. 32 91
D. 18 91
Cho hình chóp tam giác O.ABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Hãy tính đường cao OH của hình chóp.
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D trên đường tròn tâm O’ lấy điểm B, C sao cho AB//CD và AB không cắt OO’. Tính AD để thể tích khối chóp O’.ABCD đạt giá trị lớn nhất. A.
A
D
2
2
a
B. ...
Đọc tiếp
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D trên đường tròn tâm O’ lấy điểm B, C sao cho AB//CD và AB không cắt OO’. Tính AD để thể tích khối chóp O’.ABCD đạt giá trị lớn nhất.
A. A D = 2 2 a
B. A D = 4 a
C. A D = 4 3 3 a
D. A D = 2 a
Cho khối chóp S.ABC, trên ba cạnh SA, SB, SC lần lượt lấy ba điểm A, B, C sao cho SA
1
3
SA , SB
1
3
SB, SC
1
3
SC. Gọi V và V lần lượt là thể tích của các khối chóp S.ABC và S.ABC. Khi đó tỉ số
V
V
là
Đọc tiếp
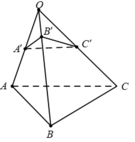
Cho khối chóp S.ABC, trên ba cạnh SA, SB, SC lần lượt lấy ba điểm
A', B', C' sao cho SA' = 1 3 SA , SB' = 1 3 SB, SC' = 1 3 SC. Gọi V và V'
lần lượt là thể tích của các khối chóp S.ABC và S.A'B'C'. Khi đó tỉ số V ' V là
![]()
![]()
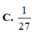
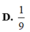
Cho A(4; 0; 0), B(0; 2; 0), C(0; 0; 1) và D(2; 2; 0). Có bao nhiêu tam giác vuông có ba đỉnh là ba trong số 5 điểm O, A, B, C, D.
Đọc tiếp
Cho A(4; 0; 0), B(0; 2; 0), C(0; 0; 1) và D(2; 2; 0). Có bao nhiêu tam giác vuông có ba đỉnh là ba trong số 5 điểm O, A, B, C, D.
![]()
![]()
![]()
![]()
Trong không gian Oxyz , lấy điểm C trên tia Oz sao cho OC 1 . Trên hai tia Ox,Oy lần lượt lấy hai điểm A,B thay đổi sao cho OA + OB OC . Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện O.ABC ?
Đọc tiếp
Trong không gian Oxyz , lấy điểm C trên tia Oz sao cho OC = 1 . Trên hai tia Ox,Oy lần lượt lấy hai điểm A,B thay đổi sao cho OA + OB = OC . Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện O.ABC ?
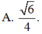
![]()
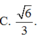
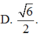
Cho hình chóp O.ABC có OA, OB, OC đôi một vuông góc tại O và OA2, OB3, OC6. Thể tích của khối chóp bằng: A. 12 B. 6 C. 24 D. 36.
Đọc tiếp
Cho hình chóp O.ABC có OA, OB, OC đôi một vuông góc tại O và OA=2, OB=3, OC=6. Thể tích của khối chóp bằng:
A. 12
B. 6
C. 24
D. 36.
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;5). Số mặt phẳng đi qua M và cắt các trục Ox, Oy, Oz tại A, B, C sao cho OA OB OC (A, B, C không trùng với gốc tọa độ O) là: A. 8 B. 3 C. 4 D. 1
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;5). Số mặt phẳng đi qua M và cắt các trục Ox, Oy, Oz tại A, B, C sao cho OA = OB = OC (A, B, C không trùng với gốc tọa độ O) là:
A. 8
B. 3
C. 4
D. 1
Cho hình chóp S.ABC. Bên trong tam giác ABC ta lấy một điểm O bất kỳ. Từ O ta dựng các đường thẳng lần lượt song song với SA, SB, SC và cắt các mặt phẳng (SBC), (SCA), (SAB) theo thứ tự tại các điểm A’, B’, C’. Tính tổng tỉ số
T
O
A
S
A
+
O
A
S
B...
Đọc tiếp
Cho hình chóp S.ABC. Bên trong tam giác ABC ta lấy một điểm O bất kỳ. Từ O ta dựng các đường thẳng lần lượt song song với SA, SB, SC và cắt các mặt phẳng (SBC), (SCA), (SAB) theo thứ tự tại các điểm A’, B’, C’. Tính tổng tỉ số T = O A ' S A + O A ' S B + O C ' S C
![]()
![]()
![]()
![]()