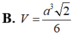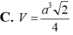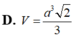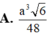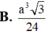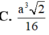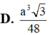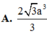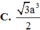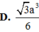Question

Cho khối chóp đều S.ABCD, đáy ABCD là hình vuông có đường chéo bằng a√2 góc giữa đường Chẳng SC và đáy bằng 30°. Tính thể tích khối chóp S.ABCD theo a. bằng

Answer 1

ABCD là hình vuông

=>\(AB^2+BC^2=AC^2\)

=>\(AB=\sqrt{\dfrac{AC^2}{2}}=\sqrt{\dfrac{\left(a\sqrt{2}\right)^2}{2}}=a\)

=>AB=BC=CD=DA=a

O là trung điểm của AC

=>\(OA=OC=\dfrac{a\sqrt{2}}{2}\)

S.ABCD là khối chóp đều

=>SO\(\perp\)(ABCD)

\(\widehat{SC;\left(ABCD\right)}=\widehat{CS;CO}=\widehat{SCO}\)

Xét ΔSOC vuông tại O có \(tanSCO=\dfrac{SO}{OC}\)

=>\(\dfrac{SO}{\dfrac{a\sqrt{2}}{2}}=tan30=\dfrac{\sqrt{3}}{3}\)

=>\(SO=\dfrac{a\sqrt{2}}{2}\cdot\dfrac{\sqrt{3}}{3}=\dfrac{a\sqrt{6}}{6}\)

\(V_{S.ABCD}=\dfrac{1}{3}\cdot SO\cdot S_{ABCD}=\dfrac{1}{3}\cdot a^2\cdot\dfrac{a\sqrt{6}}{6}=\dfrac{a^3\sqrt{6}}{18}\)