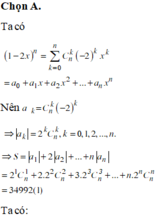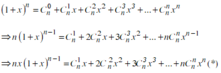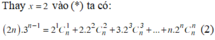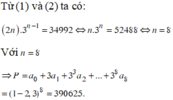Các câu hỏi tương tự
Cho hàm số
y
ln
2
x
-
a
-
2
m
ln
2
x
-
a
+
2
(m là tham số thực), trong đó x,...
Đọc tiếp
Cho hàm số y = ln 2 x - a - 2 m ln 2 x - a + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0 (với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thỏa mãn M a x 1 ; e 2 y = 1 . Số phần tử của S là:/
A. 0
B. 1
C. 2
D. Vô số
Cho
a
,
b
0,
a
≠
1,
b
≠
1,
n
∈
ℕ
*
và
P
1
log
a
b
+
1
log
a
2...
Đọc tiếp
Cho a , b > 0, a ≠ 1, b ≠ 1, n ∈ ℕ * và P = 1 log a b + 1 log a 2 b + 1 log a 3 b + ... + 1 log a n b . Một học sinh đã tính giá trị của biểu thức P như sau
Bước 1: P = log b a + log b a 2 + log b a 3 + .... + log b a n
Bước 2: P = log b a . a 2 . a 3 ... a n
Bước 3: P = log b a 1 + 2 + 3 + ... + n
Bước 4: P = n n − 1 log b a
Hỏi bạn học sinh đó đã giải sai từ bước nào?
A. Bước 1
B. Bước 3
C. Bước 2
D. Bước 4
Cho các số thực a, b, m, n sao cho
2
m
+
n
0
và thỏa mãn điều kiện
log
2
a
2
+
b
2
+...
Đọc tiếp
Cho các số thực a, b, m, n sao cho 2 m + n < 0 và thỏa mãn điều kiện log 2 a 2 + b 2 + 9 = 1 + log 2 3 a + 2 b 9 − m .3 − n .3 − 4 2 m + n + ln 2 m + n + 2 2 + 1 = 81
Tìm giá trị nhỏ nhất của biểu thức P = a − m 2 + b − n 2
A. 2 5 − 2.
B. 2.
C. 5 − 2.
D. 2 5 .
Bài 1: Cho A ( 5m2 - 8m2 - 9m2) . ( -n3 + 4n3) Với giá trị nào của m và n thì A ≥ 0 Bài 2: Cho S 1 - 3 + 32 - 33 + ... + 398 - 399 a) Chứng minh S là bội của -20 b) Tính S, từ đó suy ra 3100 chia cho 4 dư 1 Bài 3: Tìm số nguyên n sao cho: n - 1 là bội của n + 5 và n + 5 là bội của n - 1 Bài 4: Tìm số nguyên a, b biết (a,b) 24 và a + b -10Toán lớp 6 nha, giải dùm mình, mình cảm ơn
Đọc tiếp
Bài 1: Cho A = ( 5m2 - 8m2 - 9m2) . ( -n3 + 4n3)
Với giá trị nào của m và n thì A ≥ 0
Bài 2: Cho S = 1 - 3 + 32 - 33 + ... + 398 - 399
a) Chứng minh S là bội của -20
b) Tính S, từ đó suy ra 3100 chia cho 4 dư 1
Bài 3: Tìm số nguyên n sao cho:
n - 1 là bội của n + 5 và n + 5 là bội của n - 1
Bài 4: Tìm số nguyên a, b biết (a,b) = 24 và a + b = -10
Toán lớp 6 nha, giải dùm mình, mình cảm ơn
Cho hai số thực dương x, y thỏa mãn
l
o
g
3
(
x
+
y
+
2
)
1
+
l
o
g
3
x
-
1
y
+
y
-
1...
Đọc tiếp
Cho hai số thực dương x, y thỏa mãn l o g 3 ( x + y + 2 ) = 1 + l o g 3 x - 1 y + y - 1 x . Giá trị nhỏ nhất của biểu thức x 2 + y 2 x y = a b với a , b ∈ N và (a,b)=1. Hỏi a+b bằng bao nhiêu
A. 2
B. 9
C. 12
D. 13
Cho các số thực x,y thay đổi thỏa mãn
log
2
sinx
+
2
cosx
+
2
2
cosx
-
sinx
+
3
. Gọi -
a
b
...
Đọc tiếp
Cho các số thực x,y thay đổi thỏa mãn log 2 sinx + 2 cosx + 2 = 2 cosx - sinx + 3 . Gọi - a b với a ∈ N * , b ∈ N * , a b tối giản là giá trị nhỏ nhất của biểu thức P= 3 cos 3 x + sin 2 x - 5 cosx . Tính T=a+b.
A.T=200.
B. T=257.
C. T=210.
D. T=240
Khai triển và rút gọn, ta được
(
1
+
a
x
)
n
1
+
24
x
+
252
x
2
+
.
.
.
Giá trị của biểu thức a+n bằng A. 11. B. 13. C. 12. D. 9.
Đọc tiếp
Khai triển và rút gọn, ta được ( 1 + a x ) n = 1 + 24 x + 252 x 2 + . . . Giá trị của biểu thức a+n bằng
A. 11.
B. 13.
C. 12.
D. 9.
Cho a; b; n 0 và
a
≠
1
;
a
b
≠
1
.Tính giá trị của biểu thức
T
log
a
n
log
a
b
n
log
a
b
A. T 4 B. T...
Đọc tiếp
Cho a; b; n > 0 và a ≠ 1 ; a b ≠ 1 .
Tính giá trị của biểu thức T = log a n log a b n log a b
A. T = 4
B. T = 3
C. T = 2
D. T = 1
Trong không gian Oxyz, cho mặt cầu (S): (x-1)2+ (y-2)2+ z225 và một điểm A(a,b,c) nằm trên mặt cầu (S). Từ A vẽ ba tia đôi một vuông góc với nhau cắt mặt cầu (S) tại điểm thứ hai là M, N, P. Biết rằng mặt phẳng (MNP) luôn đi qua một điểm cố định K(1;1;3). Giá trị của biểu thức a + 7b + c bằng A. 3 B. 4 C. 6 D. 9
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): (x-1)2+ (y-2)2+ z2=25 và một điểm A(a,b,c) nằm trên mặt cầu (S). Từ A vẽ ba tia đôi một vuông góc với nhau cắt mặt cầu (S) tại điểm thứ hai là M, N, P. Biết rằng mặt phẳng (MNP) luôn đi qua một điểm cố định K(1;1;3). Giá trị của biểu thức a + 7b + c bằng
A. 3
B. 4
C. 6
D. 9