Các câu hỏi tương tự
Với giá trị nào của góc
φ
sau đây thì phép quay
Q
O
;
φ
biến hình vuông ABCD tâm O thành chính nó? A.
φ
π
2
B.
φ
3
π
4
C.
φ...
Đọc tiếp
Với giá trị nào của góc φ sau đây thì phép quay Q O ; φ biến hình vuông ABCD tâm O thành chính nó?
A. φ = π 2
B. φ = 3 π 4
C. φ = 2 π 3
D. φ = π 3
Cho hình vuông ABCD với O là giao điểm hai đường chéo. Tìm góc
φ
để phép quay
Q
O
;
φ
biến hình vuông ABCD thành chính nó. A.
φ
π
6
B.
φ
π
3
C.
φ
π
2
D.
φ
2...
Đọc tiếp
Cho hình vuông ABCD với O là giao điểm hai đường chéo. Tìm góc φ để phép quay Q O ; φ biến hình vuông ABCD thành chính nó.
A. φ = π 6
B. φ = π 3
C. φ = π 2
D. φ = 2 π 3
Cho hình vuông ABCD. Gọi Q là phép quay tâm A biến B thành D, Qlà phép quay tâm C biến D thành B. Khi đó, hợp thành của hai phép biến hình Q và Q(tức là thực hiện phép quay Q trước sau đó tiếp tục thực hiện phép quayQ ) là: A. Phép quay tâm B góc quay
90
°
B. Phép đối xứng tâm B C. Phép tịnh tiến theo D. Phép đối xứng trục BC.
Đọc tiếp
Cho hình vuông ABCD. Gọi Q là phép quay tâm A biến B thành D, Q'là phép quay tâm C biến D thành B. Khi đó, hợp thành của hai phép biến hình Q và Q'(tức là thực hiện phép quay Q trước sau đó tiếp tục thực hiện phép quayQ' ) là:
A. Phép quay tâm B góc quay 90 °
B. Phép đối xứng tâm B
C. Phép tịnh tiến theo
D. Phép đối xứng trục BC.
Trong năm phép biến hình: Tịnh tiến, đối xứng tâm, đối xứng trục, phép quay và phép vị tự. Có bao nhiêu phép biến hình luôn biến một đường thẳng thành đường thẳng song song hoặc trùng với nó?
A. 1
B. 2
C. 3
D. 4
Cho hình vuông ABCD có M là trung điểm của BC. Phép tịnh tiến the vecto
v
→
biến M thành A thì v bằng A.
1
2
A
D
→
+
D
C
→
B.
A
C
→
+
A...
Đọc tiếp
Cho hình vuông ABCD có M là trung điểm của BC. Phép tịnh tiến the vecto v → biến M thành A thì v bằng
A. 1 2 A D → + D C →
B. A C → + A B →
C. 1 2 C B → - A B →
D. 1 2 C B → + A B →
Cho ba điểm A, B, C thẳng hang theo thứ tự đó và AB 2BC. Dựng các hình vuông ABEF, BCGH (đỉnh của hình vuông tính theo chiều kim đồng hồ). Xét phép quay tâm B góc quay
-
90
°
biến điểm E thành điểm A. Gọi I là giao điểm của EC và GH. Giả sử I biến thành điểm J qua phép quay trên. Nếu AC 3 thì IJ bằng bao nhiêu? A.
10
2
B.
5
C.
2
5
D. ...
Đọc tiếp
Cho ba điểm A, B, C thẳng hang theo thứ tự đó và AB = 2BC. Dựng các hình vuông ABEF, BCGH (đỉnh của hình vuông tính theo chiều kim đồng hồ). Xét phép quay tâm B góc quay - 90 ° biến điểm E thành điểm A. Gọi I là giao điểm của EC và GH. Giả sử I biến thành điểm J qua phép quay trên. Nếu AC = 3 thì IJ bằng bao nhiêu?
A. 10 2
B. 5
C. 2 5
D. 10
Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k 2 và phép đối xứng tâm I biến tứ giác IGHF thành A. AIFD B. BCFI C. CIEB D. DIEA
Đọc tiếp
Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành
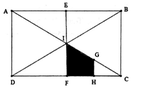
A. AIFD
B. BCFI
C. CIEB
D. DIEA
Cho hình thang ABCD có
A
B
//
C
D
,
A
B
8,
C
D
4.
Gọi I là giao điểm của hai đường chéo và J là giao điểm của hai cạnh bên. Phép biến hình biến vectơ
A
B
→
thành vectơ
C
D
→
là phép vị tự nào sau đây? A.
V...
Đọc tiếp
Cho hình thang ABCD có A B // C D , A B = 8, C D = 4. Gọi I là giao điểm của hai đường chéo và J là giao điểm của hai cạnh bên. Phép biến hình biến vectơ A B → thành vectơ C D → là phép vị tự nào sau đây?
A. V I ; 1 2
B. V J ; 1 2
C. V I ; − 1 2
D. V J ; − 1 2
Trong mặt phẳng Oxy, cho đường thẳng d: x-2y+2=0; d': x-2y-8=0. Phép đối xứng tâm biến d thành d' và biến trục Ox thành chính nó có tâm I là
A. I(0;-3)
B. I(0;3)
C. I(-3;0)
D. I(3;0)




