Đáp án C
A B C D = 1 2 ⇒ C D → = − 1 2 A B → . Vậy V I ; − 1 2 : C D → → A B →
Đáp án C

A B C D = 1 2 ⇒ C D → = − 1 2 A B → . Vậy V I ; − 1 2 : C D → → A B →
Cho ba điểm A, B, C thẳng hang theo thứ tự đó và AB = 2BC. Dựng các hình vuông ABEF, BCGH (đỉnh của hình vuông tính theo chiều kim đồng hồ). Xét phép quay tâm B góc quay - 90 ° biến điểm E thành điểm A. Gọi I là giao điểm của EC và GH. Giả sử I biến thành điểm J qua phép quay trên. Nếu AC = 3 thì IJ bằng bao nhiêu?
A. 10 2
B. 5
C. 2 5
D. 10
Cho hình vuông ABCD. Gọi Q là phép quay tâm A biến B thành D, Q'là phép quay tâm C biến D thành B. Khi đó, hợp thành của hai phép biến hình Q và Q'(tức là thực hiện phép quay Q trước sau đó tiếp tục thực hiện phép quayQ' ) là:
A. Phép quay tâm B góc quay 90 °
B. Phép đối xứng tâm B
C. Phép tịnh tiến theo
D. Phép đối xứng trục BC.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 5 ; 1 ; - 1 , B 14 ; - 3 ; 3 và đường thẳng ∆ có vectơ chỉ phương = 1 ; 2 ; 2 . Gọi C, D lần lượt là hình chiếu của A,B lên ∆ . Mặt cầu qua hai điểm C, D có diện tích nhỏ nhất là
A. 44 π
B. 6 π
C. 9 π
D. 36 π
Cho hình lập phương ABCD. A 'B 'C 'D ' có I, J tương ứng là trung điểm của BC và BB ' . Góc giữa hai đường thẳng AC và IJ bằng
A. 45 °
B. 60 °
C. 30 °
D. 120 °
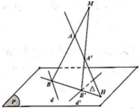
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x - 2 1 = y - 5 2 = z - 2 1 , d ' : x - 2 1 = y - 1 - 2 = z - 2 1 và hai điểm A(a;0;0), A’(0;0;b). Gọi (P) là mặt phẳng chứa d và d’; H là giao điểm của đường thẳng AA’ và mặt phẳng (P). Một đường thẳng thay đổi trên (P) nhưng luôn đi qua H đồng thời D cắt d và d’ lần lượt tại B, B’. Hai đường thẳng AB, A’B’ cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có vectơ chỉ phương u → = 15 ; - 10 ; - 1 (tham khảo hình vẽ). Tính a+b
A. 8
B. 9
C. -9
D. 6
Trong mặt phẳng tọa độ Oxy, cho hai đường tròn C ' : x 2 + y 2 + 2 m - 2 y - 6 x + 12 + m 2 = 0 và C : x + m 2 + y - 2 2 = 5 . Vectơ v → nào dưới đây là vectơ của phép tịnh tiến biến (C) thành (C')
A. v → = 2 ; 1
B. v → = - 2 ; 1
C. v → = - 1 ; 2
D. v → = 2 ; - 1
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
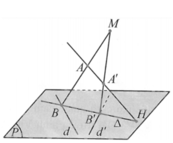
d : x - 2 1 = y - 5 2 = z - 2 1 , d ' : x - 2 1 = y - 1 - 2 = z - 2 1 và hai điểm A a ; 0 ; 0 , A ' 0 ; 0 ; b . Gọi (P) là mặt phẳng chứa d và d '; H là giao điểm của đường thẳng AA' và mặt phẳng (P). Một đường thẳng ∆ thay đổi trên (P) nhưng luôn đi qua H đồng thời ∆ cắt d và d ' lần lượt là B, B '. Hai đường thẳng AB, A'B' cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có vectơ chỉ phương u → = 15 ; - 10 ; - 1 (tham khảo hình vẽ). Tính T= a+b
A. T = 8
B. T = 9
C. T = - 9
D. T = 6
Cho hình hộp ABCD.A’B’C’D’ có A(1;0;0), B(2;-1;1), D(0;1;1) và A’(1;2;1). Gọi M, N, P, Q, E, F lần lượt là giao điểm của hai đường chéo của sáu mặt hình hộp. Tính thể tích của V khối đa diện lồi hình thànhbởi sáu điểm M, N, P, Q, E, F.
A. V = 1 3
B. V = 1 2
C. V = 2 3
D. V = 1
trong mặt phẳng tọa độ oxy cho hình thang cân ABCD( AB song song với CD) có tọa độ đỉnh A(2,-1).giao điểm của 2 đường chéo AC và BD là I(1,2).đường tròn ngoại tiếp tam giác ADI có tâm E(-27/8,-9/8),biết đường thẳng BC qua M(9,-6).tìm B,D , biết B có tung độ nhỏ hơn 3