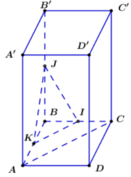
Gọi K là trung điểm của AB ⇒ IK // BC (tính chất đường trung bình của tam giác)
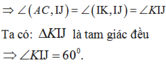
Chọn B.

Gọi K là trung điểm của AB ⇒ IK // BC (tính chất đường trung bình của tam giác)
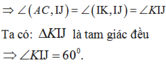
Chọn B.
Cho hình lập phương ABCD.A'B'C'D' có I, J tương ứng là trung điểm của BC và BB’. Góc giữa hai đường thẳng AC và IJ bằng
A. 30 °
B. 60 °
C. 90 °
D. 45 °
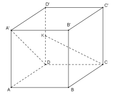
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1. Gọi K là trung điểm của DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CK và A′D bằng
A. 10 5
B. 4 5
C. 10 10
D. 2 5
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B′C′ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B′D′ bằng
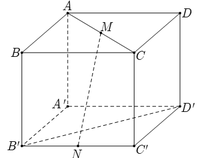
A. 5 a 5
B. a 3
C. 5 a
D. 3 a
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = 2 a , B C = a . Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AB, góc giữa đường thẳng SC và mặt phẳng đáy bằng 60 ° Tính góc giữa hai đường thẳng SB và AC.
A. 60 °
B. 19 ° 45 ' 31 , 78 ' '
C. 70 ° 14 ' 28 , 22 ' '
D. 57 ° 41 ' 18 , 48 ' '
Cho hình lăng trụ A B C . A ' B ' C ' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A’ trên (ABC) là trung điểm của AB, góc giữa A’C và mặt đáy bằng 60 ° . Khoảng cách giữa hai đường thẳng AC và BB’ bằng
A. 6 a 52
B. 3 a 52
C. a 3 4
D. 4 a 3
Cho hình lập phương ABCD.A′B′C′D′ cạnh bằng a. Gọi M là trung điểm cạnh DD′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng CB′ và MC′ bằng
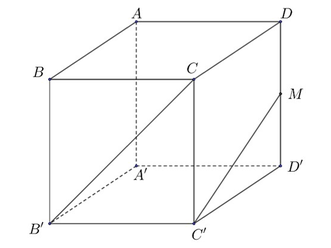
A. 2 2 9
B. 10 10
C. 2 9
D. 10 5
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Góc giữa hai đường thẳng AB′ và BC′ bằng (tham khảo hình vẽ bên).
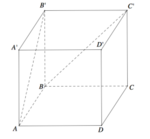
A. 60 °
B. 90 °
C. 45 °
D. 300 °
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Góc giữa hai đường thẳng AB′ và BC′ bằng (tham khảo hình vẽ bên).

A. 60 °
B. 90 °
C. 45 °
D. 30 °
Cho hình lăng trụ ABCA’B’C’ có đáy tam giác đều cạnh a. Hình chiếu vuông góc của A’ trên (ABC) là trung điểm của AB, góc giữa A’C và mặt đáy bằng 60 ° . Tính khoảng cách h giữa hai đường thẳng AC và BB
A. h = 6 a 52
B. h = 3 a 52
C. a 3 4
D. 4 a 3