Các câu hỏi tương tự
Cho tam giác ABC nhọn có AB<AC và nội tiếp đươngf tròn O đường kính AD. Gọi AH là đường cao của tam giác ABC. Qua B kẻ đường thẳng vuông góc với đường thẳng AD tại E.
a) cm: 2 HE vuong góc với AC
b) gọi F là hình chiếu vuông góc của điểm C lên đường thẳng AD và M là trung điểm của BC. Chứng minh M là tâm dường tròn ngoại tiếp tam giác HEF
Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt trung điểm của AB, AC và BC. Gọi O là giao điểm của ba đường phân giác trong tam giác ABC. Khi đó, tâm đường tròn ngoại tiếp tam giác ABC là:
A. O
B. D
C. E
D. F
Cho tam giác ABC vuông tại A (AC < AB) có BD là phân giác. E là hình chiếu của D lên BC.
a) Chứng minh tam giác ABD = tam giác EBD.
b) Gọi F là giao điểm của BA và ED. Chứng minh tam giác FBC cân.
c) Chứng minh AC + AE > FC + AE.
d) Gọi D là giao điểm của BD và FC, trên đoạn BF lấy điểm J sao cho 3BJ = BF, H là giao điểm của GJ và CB. Chứng minh J là trọng tâm của tam giác CHF
Cho tam giác ABC có AB = AC. Gọi I và J lần lượt là trung điểm của
AB và AC
a) Chứng minh
b) Gọi O là giao điểm của BJ và CI. Chứng minh tam giác OBC có hai góc
bằng nhau
c) Chứng minh IJ // BC
d) Lấy điểm E và F mà I và J lần lượt là trung điểm của CE và BF. Chứng
minh A là trung điểm của EF
Cho tam giác ABC có AB = AC. Gọi I và J lần lượt là trung điểm của
AB và AC
a) Chứng minh
b) Gọi O là giao điểm của BJ và CI. Chứng minh tam giác OBC có hai góc
bằng nhau
c) Chứng minh IJ // BC
d) Lấy điểm E và F mà I và J lần lượt là trung điểm của CE và BF. Chứng
minh A là trung điểm của EF
cho tam gics ABC có ba góc nhọn, nội tiếp đường tròn tâm O (ABAC). Các đường cao AD và CF của tam gics ABC cắt nhau tại H.a) chứng minh tứ giác BFHD nội tiếp. Suy ra góc AHC 180-ABCb) gọi M là điểm bất kì trên cung nhỏ BC của đường tròn (O) (M khác B và C) và N là điểm đối xứng của M qua AC. Chứng minh tứ giác AHCN nội tiếp c) gọi I là giao điểm của AM và HC: J là giao điểm của AC và HN. Chứng minh góc AJI ANC
Đọc tiếp
cho tam gics ABC có ba góc nhọn, nội tiếp đường tròn tâm O (AB<AC). Các đường cao AD và CF của tam gics ABC cắt nhau tại H.
a) chứng minh tứ giác BFHD nội tiếp. Suy ra góc AHC= 180-ABC
b) gọi M là điểm bất kì trên cung nhỏ BC của đường tròn (O) (M khác B và C) và N là điểm đối xứng của M qua AC. Chứng minh tứ giác AHCN nội tiếp
c) gọi I là giao điểm của AM và HC: J là giao điểm của AC và HN. Chứng minh góc AJI= ANC
Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn tâm O (AB AC). Các đường cao AD và CF của tam giác ABC cắt nhau tại H.a. Chứng minh tứ giác BFHD nội tiếp. Suy ra góc AHC 180o - ABC.b. Gọi M là điểm bất kì trên cung nhỏ BC của đường tròn (O) (M khác B và C) và N là điểm đối xứng của M qua AC. Chứng minh tứ giác AHCN nội tiếp.c. Gọi I là giao điểm của AM và HC; J là giao điểm của AC và HN. Chứng minh góc AJI ANC.d. Chứng minh rằng: OA vuông góc với IJ.
Đọc tiếp
Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn tâm O (AB < AC). Các đường cao AD và CF của tam giác ABC cắt nhau tại H.
a. Chứng minh tứ giác BFHD nội tiếp. Suy ra góc AHC = 180o - ABC.
b. Gọi M là điểm bất kì trên cung nhỏ BC của đường tròn (O) (M khác B và C) và N là điểm đối xứng của M qua AC. Chứng minh tứ giác AHCN nội tiếp.
c. Gọi I là giao điểm của AM và HC; J là giao điểm của AC và HN. Chứng minh góc AJI = ANC.
d. Chứng minh rằng: OA vuông góc với IJ.
Cho tam giác ABC vuông tại A ( AB < AC ) Đường cao AH. Trong nửa mặt phẳng bờ AH vẽ hình vuông AHCE.
a) CHứng minh K thuộc đoạn HC.
b) Gọi P là giao điểm của AC và KE. Chứng minh tam giác ABP vuông cân.
c) Dựng hình bình hành APQB và gọi I là tâm hình bình hành. C/m H, I, E thẳng hàng.
Vẽ hình giùm mik nha
Cho hình vẽ:Cho đường tròn (I;r) nội tiếp tam giác ABC tiếp xúc với BC, CA, AB lần lượt tại D, E, F. DN, EK, FL là các đường kính của (I). Qua N kẻ đường thẳng song song với BC cắt AC, AB lần lượt tại P và Q. a. Chứng minh: ∆BIQ vuông và QN BD r² b. Gọi M là trung điểm của BC. Chứng minh: AN // IM c. KL cắt BC tại S. Chứng minh; SI _|_ IM
Đọc tiếp
Cho hình vẽ:
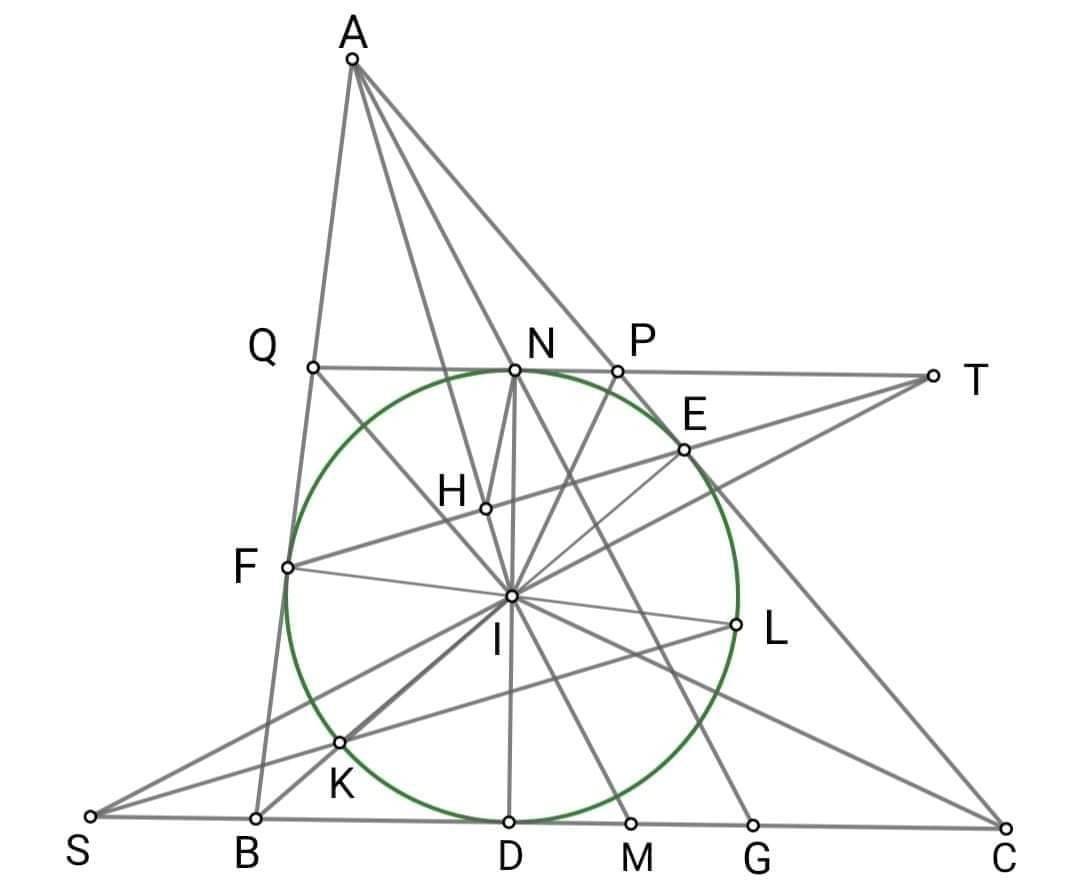 Cho đường tròn (I;r) nội tiếp tam giác ABC tiếp xúc với BC, CA, AB lần lượt tại D, E, F. DN, EK, FL là các đường kính của (I). Qua N kẻ đường thẳng song song với BC cắt AC, AB lần lượt tại P và Q. a. Chứng minh: ∆BIQ vuông và QN BD = r² b. Gọi M là trung điểm của BC. Chứng minh: AN // IM c. KL cắt BC tại S. Chứng minh; SI _|_ IM
Cho đường tròn (I;r) nội tiếp tam giác ABC tiếp xúc với BC, CA, AB lần lượt tại D, E, F. DN, EK, FL là các đường kính của (I). Qua N kẻ đường thẳng song song với BC cắt AC, AB lần lượt tại P và Q. a. Chứng minh: ∆BIQ vuông và QN BD = r² b. Gọi M là trung điểm của BC. Chứng minh: AN // IM c. KL cắt BC tại S. Chứng minh; SI _|_ IM