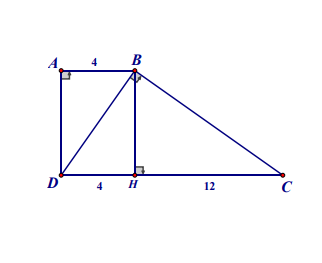
Áp dụng HTL:
\(BH^2=DH\cdot HC=48\Leftrightarrow BH=4\sqrt{3}\left(cm\right)\)
Dễ thấy ABHD là hcn nên \(BH=AD=4\sqrt{3}\left(cm\right)\)
Ta có:
\(\tan\widehat{ABD}=\dfrac{AD}{AB}=\dfrac{4\sqrt{3}}{4}=\sqrt{3}=\tan60^0\\ \Leftrightarrow\widehat{ABD}=60^0\\ \Leftrightarrow\widehat{ABC}=\widehat{ABD}+\widehat{CBD}=60^0+90^0=150^0\)