a, AD giao BC= M
AF giao BC = N
=> BEC giao ADF tại MN
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hai hình thang ABCD và ABEF có chung đáy lớn AB và không cùng nằm trong một mặt phẳng.a) Tìm giao tuyến của các mặt phẳng sau: (AEC) và (BFD), (BCE) và (ADF).b) Lấy điểm M thuộc đoạn DF. Tìm giao điểm của đường thẳng AM với mặt phẳng (BCE).c) Chứng minh hai đường thẳng AC và BF không cắt nhau.
Đọc tiếp
Cho hai hình thang ABCD và ABEF có chung đáy lớn AB và không cùng nằm trong một mặt phẳng.
a) Tìm giao tuyến của các mặt phẳng sau: (AEC) và (BFD), (BCE) và (ADF).
b) Lấy điểm M thuộc đoạn DF. Tìm giao điểm của đường thẳng AM với mặt phẳng (BCE).
c) Chứng minh hai đường thẳng AC và BF không cắt nhau.
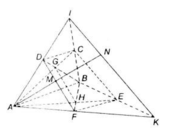
Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt .Gọi O là giao điểm của AC và BD, O’ là giao điểm của AE và BF.
a) Chứng minh rằng OO’ song song với hai mặt phẳng (ADF) và (BCE)
b) Gọi M và N lần lượt là trọng tâm của các tam giác ABDvà ABE. Chứng minh rằng .
Cho hai hình bình hành ABCD và ABEF có tâm lần lượt là O, O’ và không cùng nằm trong một mặt phẳng. gọi M là trung điểm của AB.(I) (ADF) // (BCE) (II) (MOO’) // (ADF)(III) (MOO’) // (BCE) (IV) (AEC) // (BDF)Khẳng định nào sau đây là đúng A.chỉ có (1) đúng B. chỉ có (1) và (2) đúng C. (I), (II), (III) đúng D. chỉ có (1) và (IV) đúng
Đọc tiếp
Cho hai hình bình hành ABCD và ABEF có tâm lần lượt là O, O’ và không cùng nằm trong một mặt phẳng. gọi M là trung điểm của AB.
(I) (ADF) // (BCE) (II) (MOO’) // (ADF)
(III) (MOO’) // (BCE) (IV) (AEC) // (BDF)
Khẳng định nào sau đây là đúng
A.chỉ có (1) đúng
B. chỉ có (1) và (2) đúng
C. (I), (II), (III) đúng
D. chỉ có (1) và (IV) đúng
Cho hình tứ giác ABCD có các cặp cạnh đối không song song, S là 1 điểm không nằm trong mặt phẳng ABCD, M là 1 điểm nằm trên cạnh SA a) tìm giao tuyến của 2 mặt phẳng (SAB) và (MCD) b) gọi M là trọng tâm của tam giác SCD. Tìm giao điểm của đường thẳng MG và (ABCD)
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.
a) Gọi O và O’ lần lượt là tâm của các hình bình hành ABCD và ABEF. Chứng minh rằng đường thẳng OO’ song song và các mặt phẳng (ADF) và (BCF)
b) Gọi M và N lần lượt là trọng tâm của tam giác ABD và ABE. Chứng minh đường thẳng MN song song với mặt phẳng (CEF).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, E, F lần lượt là trung điểm SB, SD và I là điểm nằm trên đoạn AB sao cho IA-3IB. O là giao điểm của AC và BD. a) Tìm giao tuyến của mp(SAC) và mp(SBD); giao tuyến của mp (SEF) và mp (ACD). b) Tìm giao tuyến của (ABCD) và (AEF). c) Tìm giao điểm H của SA và mp (EFI); giao điểm K của IF và (SAC). NỐT LUN CÂU NÀY KU Ạ , EM XIN CẢM TẠ
Cho hình chóp S. ABCD có đáy ABCD là tứ giác a). Tìm giao tuyến của (SAD) và (SBC) ? b). Tìm giao tuyến của (SAB) và (SDC) ? c). Gọi M;N là trung điểm của AD và DC. Chứng minh MN// (SAC) ? d) . Gọi K là điểm nằm bên cạnh SB. Tìm giao điểm của NK và mạ QT phẳng (SAC)
Cho tứ diện ABCD. Trên AB,AC lấy 2 điểm M,N sao cho MN không song song BC. Gọi O là một điểm nằm trong tam giác BCD. a) Tìm giao tuyến (OMN) và (BCD) b) Tìm giao điểm DB,DC, DA với (OMN) Vẽ hình giúp luôn ạ. Em cảm ơn
Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các đường chéo AC và BF lần lượt lấy các điểm M và N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M và N lần lượt cắt AD và AF tại M’ và N’. Chứng minh
a) (ADF) // (BCE).
b) M′N′ // DF.
c) (DEF) // (MM′N′N) và MN // (DEF).