Question

Cho hai hình thang ABCD và ABEF có chung đáy lớn AB và không cùng nằm trong một mặt phẳng.

a) Tìm giao tuyến của các mặt phẳng sau: (AEC) và (BFD), (BCE) và (ADF).

b) Lấy điểm M thuộc đoạn DF. Tìm giao điểm của đường thẳng AM với mặt phẳng (BCE).

c) Chứng minh hai đường thẳng AC và BF không cắt nhau.

Answer 1

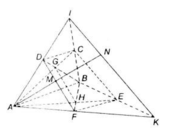
a) Giao tuyến của các cặp mặt phẳng

*Giao tuyến của (AEC) và (BFD)

• Trong hình thang ABCD, AC cắt DB tại G, ta có:

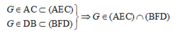
Tương tự, AE cắt BF tại H,

Ta có :

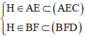 ⇒ H ∈ (AEC) ∩ (BFD).

Vậy GH = (AEC) ∩ (BFD)

*Giao tuyến của (BCE) và (ADF)

Trong hình thang ABCD, BC cắt AD tại I, ta có: I ∈ (BCE) ∩ (ADF)

Trong hình thang ABEF, BE cắt AF tại K, ta có: K ∈ (BCE) ∩ (ADF)

Vậy IK = (BCE) ∩ (ADF)

b) Giao điểm của AM với mp(BCE)

Trong mp(ADF), AM cắt IK tại N, ta có:

N ∈ IK ⊂ (BCE)

Vậy N = AM ∩ (BCE).

c) Giả sử AC cắt BF.

⇒ Qua AC và BF xác định duy nhất 1 mặt phẳng.

Mà qua A và BF có duy nhất mặt phẳng (ABEF)

⇒ AC ⊂ (ABEF)

⇒ C ∈ (ABEF) (Vô lý).

Vậy AC và BF không cắt nhau.