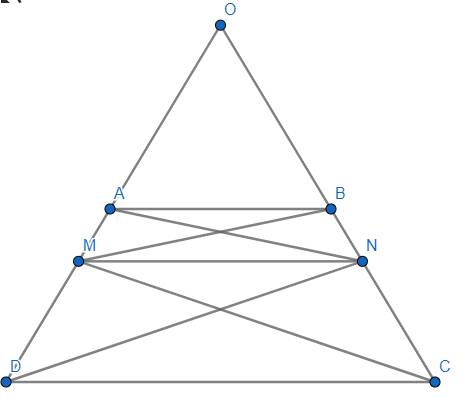
(a) Cho \(AD\cap BC=\left\{O\right\}.\) Do \(AB\left|\right|CD\left(gt\right)\Rightarrow\hat{OAB}=\hat{ODC}=\hat{OCD}=\hat{OBA}\) (đồng vị và tính chất hình thang cân) \(\Rightarrow\Delta OAB\) cân tại \(O\Rightarrow OA=OB.\)
Mà: \(AM=BN\Rightarrow OA+AM=OB+BN\Leftrightarrow OM=ON\Rightarrow\Delta OMN\) cân tại \(O\Rightarrow\hat{OMN}=\hat{ONM}=\dfrac{180^o-\hat{O}}{2}\left(1\right)\).
Lại có \(\Delta OAB\) cân tại \(O\left(cmt\right)\Rightarrow\hat{OAB}=\hat{OBA}=\dfrac{180^o-\hat{O}}{2}\left(2\right)\)
Từ (1) và (2), suy ra: \(\hat{OMN}=\hat{OAB}\Rightarrow AB\left|\right|MN\).
Mà: \(AB\left|\right|CD\left(gt\right)\Rightarrow AB\left|\right|MN\left|\right|CD\left(3\right)\)
Từ (1) và (3) \(\Rightarrow ABNM\) là hình thang cân (đpcm).
Mặt khác: \(\hat{MDC}=\hat{NCD}\left(gt\right)\left(4\right)\)
Từ (3) và (4) \(\Rightarrow MNCD\) là hình thang cân (đpcm).