Xét ΔCAB có IF//AB
nên CF/CB=CI/CA=1/2
=>F là trung điểm của BC
Xét ΔADC có
I là trung điểm của AC
IE//DC
=>E là trung điểm của AD
Xét hình thang ABCD có
E,F lần lượt là trung điểm của AD,BC
=>EF//AB//CD
=>AE/AD=BF/BC=CF/CB
Xét ΔCAB có IF//AB
nên CF/CB=CI/CA=1/2
=>F là trung điểm của BC
Xét ΔADC có
I là trung điểm của AC
IE//DC
=>E là trung điểm của AD
Xét hình thang ABCD có
E,F lần lượt là trung điểm của AD,BC
=>EF//AB//CD
=>AE/AD=BF/BC=CF/CB
cho Hình thang ABCD có AB // CD O là giao điểm của AC và BD a, chứng mình OA/AC = OB/BD. b, Kẻ đường thẳng đi qua O song song với AD cắt CD tại E. Đường thẳng đi qua O song song với BC cắt CD tại F. Chứng minh DE = CF. c, Gọi I là giao điểm của AD và FO, J là giao điểm của BC và EO. Chứng mình IJ // AB. d, Gọi H là giao điểm của AD và BC K là trung điểm của EF. chứng mminhf O,H,K thẳng hàng
Cho hình thang ABCD (AB // CD, AB < CD) .Gọi O là giao điểm của AC và BD
a) Chứng minh OA/AC = OB/BD ( làm được r)
b) Qua O kẻ đường thẳng // với AD cắt DC ở E, qua O kẻ đường thẳng // với BC cắt DC ở F. Chứng minh DE = CF
c) Gọi I là giao điểm của các đường thẳng AD và OF, J là giao điểm của các đường thẳng BC và OE. Chứng minh IJ//AB
d) Gọi H là giao điểm của AD và BC, K là trung điểm của EF. Chứng minh : H,O,K thẳng hàng
Cho hình ở trên, biết ABCD là hình thang (AB // CD). E là trung điểm của AD, qua E kẻ đường song song với 2 đáy và cắt AC tại I, cắt BC tại F. Chứng minh: a) I là trung điểm của AC. b) F là trung điểm của BC.
GIÚP MÌNH VỚI Ạ MÌNH CẢM ƠN
Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD tại I, cắt AC ở K. AK=KC ; BI = ID. Chứng minh rằng: IK = CD/2 - AB/2
Cho hình thang ABCD ( AB//CD), Gọi M,N lần lượt là trung điểm của AB<CD, O là giao điểm của AC và BD; I là giao điểm của AD,BC
a) chứng minh O,I,M,N thẳng hàng
b) Qua O kẻ đường thẳng song song với AB cắt AD,BC lần lượt tại E,F. Chứng minh OE=OF
ho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD tại I, cắt AC ở K. a) Chứng minh rằng: AK = KC, BI = ID. b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK.
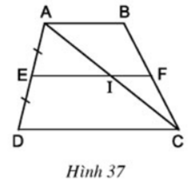
Cho hình thang ABCD (AB // CD). Qua trung điểm E của AD kẻ đường thẳng song song với hai đáy, đường thẳng này cắt AC ở I, cắt BC ở F (h.37). Có nhận xét gì về vị trí của điểm I trên AC, điểm F trên BC ?
Cho hình thang ABCD với AB song song CD, AB<CD. Gọi trung điểm của đường chéo BD là M. Qua M kẻ đường thẳng song song với DC cắt AC tại N. Gọi E là trung điểm của AB, O là giao điểm của AD và BC, OE cắt CD tại F. Chứng minh F là trung điểm của CD.
Cho hình thang ABCD có AB//CD (AB<CD), M là trung điểm AD. Qua M vẽ đường thẳng // với 2 đáy của hình thang cắt 2 đường chéo BD và AC lần lượt tại E,F.
a) Chứng minh N, E, F lần lượt là trung điểm của BC, BD, AC
b) Gọi I là trưng điểm AB, đường thẳng vuông góc với IE cắt với nhau tại E và đường thẳng vuông góc với IF tại F cắt nhau tại K. Chứng minh KC=KD