Chọn đáp án B
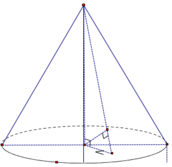
Gọi I là trung điểm AB.
Ta có
![]()
Trong (SOI), kẻ OH ⊥ SI thì OH ⊥ (SAB)
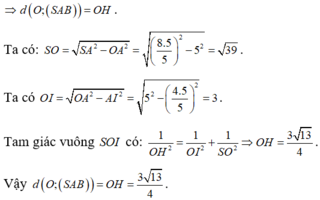
Chọn đáp án B

Gọi I là trung điểm AB.
Ta có
![]()
Trong (SOI), kẻ OH ⊥ SI thì OH ⊥ (SAB)
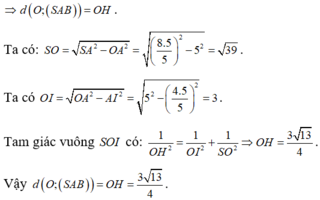
Cho hình nón đỉnh S, đáy là đường tròn (O;r). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho SA = AB = 8 r 5 . Tính theo r khoảng cách từ O đến (SAB)
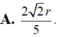
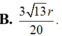
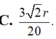
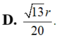
Cho hình nón tròn xoay có đường cao h = 40 (cm), bán kính đáy r = 50 (cm). Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 24 (cm). Tính diện tích của thiết diện
A. S = 800 c m 2
B. S = 1200 c m 2
C. S = 1600 c m 2
D. S = 2000 c m 2
Cho hình nón đỉnh S. Xét hình chóp S.ABC có đáy ABC là tam giác ngoại tiếp đường tròn đáy của hình nón và có AB= BC= 10a, AC= 12a, góc tạo bởi hai mặt phẳng(SAB) và ( ABC) bằng 60 0 . Tính thể tích khối nón đã cho.
A. 9 π a 3
B. 27 π a 3
C.3 π a 3
D. 12 π a 3
Cho hình nón đỉnh S. Xét hình chóp S.ABC có đáy ABC là tam giác ngoại tiếp đường tròn đáy của hình nón và AB=BC=10a, AC=12a , góc tạo bởi hai mặt phẳng (SAB)) và (ABC) bằng 45 o C Thể tích khối nón đã cho bằng
A. 9 πa 3
B. 12 πa 3
C. 27 πa 3
D. 3 πa 3
Cho hình nón có chiều cao bằng 2. Gọi ( α ) là mặt phẳng đi qua đỉnh S của hình nón và cắt mặt đáy hình nón theo một dây cung AB và tạo với đáy hình nón một góc π 4 . Tính diện tích của mặt cắt SAB. Biết dây cung AB có số đo 2 π 3 .
A . 4 6
B . 2 6
C . 4 3
D . 4 2
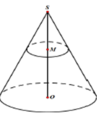
Một hình nón có chiều cao SO=50cm và có bán kính đáy bằng 10cm Lấy điểm M thuộc đoạn SO sao cho OM=20cm Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn (C). Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi (C) (xem hình vẽ).
![]()
![]()
![]()
![]()
Xét một hình trụ nội tiếp trong hình nón như hình bên, trong đó S là đỉnh hình nón, O là tâm đường tròn mặt đáy. Các đoạn AB, CD lần lượt là đường kính của đường tròn đáy của hình nón và hình trụ. Biết AC, BD cắt nhau tại điểm M (M ∈ SO) tỉ số thể tích của hình trụ và hình nón là 4 9 . Tính tỉ số S M S O

A. 7 9
B. 2 3
C. 4 5
D. 5 6
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a, khoảng cách từ tâm O của đường tròn ngoại tiếp của đáy ABC đến một mặt bên là a 2 . Thể tích của khối nón đỉnh S đáy là đường tròn ngoại tiếp tam giác ABC bằng:
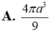
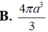
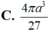
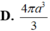
Cho hình nón tròn xoay có chiều cao h = 20 cm, bán kính đáy r = 25 cm.. Mặt phẳng ( α ) đi qua đỉnh của hình nón cách tâm của đáy 12 cm Tính diện tích thiết diện của hình nón cắt bởi mặt phẳng ( α ) .
A. S = 400 ( c m 2 )
B. S = 406 ( c m 2 )
C. S = 300 ( c m 2 )
D. S = 500 ( c m 2 )