Đáp án A
Gọi SAB là thiết diện qua trục của hình nón.
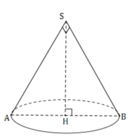

Đáp án A
Gọi SAB là thiết diện qua trục của hình nón.


Cho hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng 2a. Thể tích khối nón đã cho bằng
A. 2 2 π a 3 3
B. 2 2 π a 3
C. 8 2 π a 3 3
D. 2 2 π a 2 3
Cho hình nón (N) có thiết diện qua trục là tam giác vuông cân, cạnh bên bằng 2a. Tính thể tích của khối nón (N) theo a.
A. 2 πa 3 2
B. 2 πa 3 2 3
C. πa 3 3
D. πa 3
Thiết diện qua trục của một hình nón (N) là một tam giác vuông cân, có cạnh góc vuông bằng a diện tích toàn phần của hình nón (N) bằng:
A. π 2 a 2 2
B. π 1 + 2 a 2 2
C. π 1 + 3 a 2 2
D. π a 2 2
Thiết diện qua trục của hình nón (N) là tam giác vuông cân có cạnh góc vuông bằng a. Tính diện tích toàn phần của hình nón (N)
A. S t p = π a 2 2 + 2 2
B. S t p = π a 2 2 + 1 2
C. S t p = π a 2 1 + 2
D. S t p = π a 2 1 + 2 2 2
Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh huyền bằng 2 3 . Thể tích của khối nón đã cho bằng
A. π 3
B. 3 π
C. 3 π 2
D. 3 π 3
Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh huyền bằng 2 3 . Thể tích của khối nón này bằng
A. π 3
B. 3 π 3
C. 3 π
D. 3 π 2
Tính thể tích của vật thể giới hạn bởi hai mặt phẳng x = 0 , x = π . Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ x 0 ≤ x ≤ π là một tam giác vuông cân có cạnh huyền bằng sin x + 2
A. 7 π 6 + 2
B. 7 π 6 + 1
C. 9 π 8 + 2
D. 9 π 8 + 1
Cho khối nón có thiết diện qua trục là tam giác cân có một góc 120 ° và cạnh bên bằng a . Tính thể tích khối nón
A. π a 3 8
B. 3 π a 3 8
C. π a 3 3 24
D. π a 3 4
Cho hình nón có thiết diện qua trục của hình nón là tam giác vuông cân có cạnh góc vuông bằng a 2 . Diện tích xung quanh của hình nón bằng:
A. π a 2 2 3
B. π a 2 2 2
C. 2 2 π a 2
D. 2 π a 2