Đáp án D
Do M C A ' C = 3 4 ⇒ d N ; A B C d M ; A B C = 3 4
Ta có
V M . A B C D = 1 3 S A B C D . d M ; A B C D = 1 3 S A B C D . 3 4 d A ; A B C D = 1 4 V A B C D . A ' B ' C ' D ' ⇒ V 1 V 2 = 1 4
Đáp án D

Do M C A ' C = 3 4 ⇒ d N ; A B C d M ; A B C = 3 4
Ta có
V M . A B C D = 1 3 S A B C D . d M ; A B C D = 1 3 S A B C D . 3 4 d A ; A B C D = 1 4 V A B C D . A ' B ' C ' D ' ⇒ V 1 V 2 = 1 4
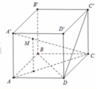
Cho hình lập phương ABCD.A'B'C'D'. Gọi M là điểm trên đường chéo CA' sao cho M C → = - 3 M A ' → . Tính tỉ số giữa thể tích V 1 của khối chóp M.ABCD và thể tích V 2 của khối lập phương.
A. V 1 V 2 = 1 3
B. V 1 V 2 = 3 4
C. V 1 V 2 = 1 9
D. V 1 V 2 = 1 4
Cho hình lăng trụ A B C . A ' B ' C ' có thể tích là V . Điểm M nằm trên cạnh A A ' sao cho A M = 2 M A ' . Gọi V ' là thể tích của khối chóp M . B C C ' B ' M.BCC’B’. Tính tỉ số V ' V .
A. V ' V = 1 3
B. V ' V = 1 2
C. V ' V = 3 4
D. V ' V = 2 3
Tính thể tích V của khối lập phương ABCD.A’B’C’D’ biết đường chéo A C ' = a 3
A. a 3 3
B. 3 3 a 3
C. 3 6 a 3 4
D. a 3
Cho hình hộp ABCD.A’B’C’D’ có A(1;0;0), B(2;-1;1), D(0;1;1) và A’(1;2;1). Gọi M, N, P, Q, E, F lần lượt là giao điểm của hai đường chéo của sáu mặt hình hộp. Tính thể tích của V khối đa diện lồi hình thànhbởi sáu điểm M, N, P, Q, E, F.
A. V = 1 3
B. V = 1 2
C. V = 2 3
D. V = 1
Cho hình chóp S.ABC có S A = S B = S C = 3 , tam giác ABC vuông cân tại B và
A C = 2 2 . Gọi M, N lần lượt là trung điểm của AC và BC. Trên hai cạnh SA, SB lấy các điểm P, Q tương ứng sao cho S P = 1 , S Q = 2. Tính thể tích V của khối tứ diện M N P Q .
A. V = 7 18
B. V = 3 12
C. V = 34 12
D. V = 34 144
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Gọi M, N lần lượt nằm trên các cạnh A ' B ' và BC sao cho M A ' = M B ' và NB = 2NC. Mặt phẳng (DMN) chia khối lập phương đã cho thành hai khối đa diện. Gọi V H là thể tích khối đa diện chứa đỉnh A, V ( H ' ) là thể tích khối đa diện còn lại. Tỉ số V H V H ' bằng
A. 151 209
B. 209 360
C. 2348 3277
D. 151 360
Khối hộp chữ nhật ABCD.A’B’C’D’ có độ dài AD, AD’, AC’ lần lượt là 1; 2; 3. Tính thể tích V của khối chóp A.A’B’C’D’.
![]()
![]()
![]()
![]()
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Tính thể tích V của khối chóp D ' . A B C D .
A. V = a 3 4
B. V = a 3 6
C. V = a 3 3
D. V = a 3
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có thể tích là V. Gọi M là một điểm trên cạnh AB sao cho M A A B = x , 0 < x < 1 . Biết rằng mặt phẳng α qua M và song song với (SBC) chia khối chóp S.ABCD thành hai phần trong đó phần chứa điểm A thể tích bằng 4 27 V . Tính giá trị của biểu thức P = 1 − x 1 + x
A. 1/2
B. 1/5
C. 1/3
D. 3/5