Gọi ![]()
Suy ra OI//AB'. Khi đó ![]()
Ta có ![]()
Suy ra ![]()
![]()
Chọn C.
Gọi ![]()
Suy ra OI//AB'. Khi đó ![]()

Ta có ![]()
Suy ra ![]()
![]()
Chọn C.
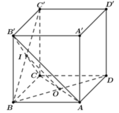
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Tính theo a khoảng cách giữa hai đường thẳng A B ' và B C ' .
A. a 3 3
B. a 2 3
C. a 3 2
D. a 2 2
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Góc giữa hai đường thẳng AB′ và BC′ bằng (tham khảo hình vẽ bên).
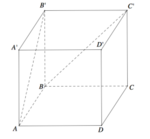
A. 60 °
B. 90 °
C. 45 °
D. 300 °
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Góc giữa hai đường thẳng AB′ và BC′ bằng (tham khảo hình vẽ bên).

A. 60 °
B. 90 °
C. 45 °
D. 30 °
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Góc giữa hai đường thẳng A'B và AC' bằng
A. 60 ° .
B. 30 ° .
C. 90 ° .
D. 45 ° .
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB và C'D' bằng
A. a
B. a 2
C. a 3 2
D. a 3
Cho hình lăng trụ tam giác đều ABCD.A'B'C'D' có bán kính đường tròn ngoại tiếp đáy ABC bằng 2 a 3 3 và góc giữa hai đường thẳng AB' và BC' bằng 60 ∘ . Tính khoảng cách d giữa hai đường thẳng AB' và BC' ?
A. d = 2 2 a 3
B. d = 4 a 3
C. d = 2 3 a 3
D. d = 2 6 a 3
Cho hình hộp A B C D . A ' B ' C ' D ' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60 ∘ . Tính khoảng cách giữa hai đường thẳng A B ' v à A ' C '
A. 22 11
B. 2 11
C. 2 11
D. 3 11
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a, gọi α là góc giữa đường thẳng AB' và mặt phẳng (BB'D'D). Tính sin α .
A. 3 4 .
B. 3 2 .
C. 3 5 .
D. 1 2 .
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và A'C' bằng
A. a
B. a 2
C. 3 a 2
D. 3 a