Các câu hỏi tương tự
Cho hình lập phương a 1 có cạnh bằng a 1. Một đường thẳng d đi qua đỉnh D và tâm I cuả mặt bên BCCB. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCCB) và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d ( tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là: A. a 1 B. a
1
2
C.
a
2
5
D.
a...
Đọc tiếp
Cho hình lập phương a = 1 có cạnh bằng a = 1. Một đường thẳng d đi qua đỉnh D ' và tâm I cuả mặt bên BCC'B'. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCC'B') và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d ( tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là:
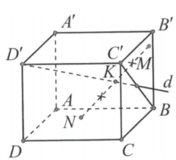
A. a =1
B. a = 1 2
C. a = 2 5
D. a = 1 3
Cho hình lập phương ABCD.A’B’C’D’ có các cạnh bằng 1. M là trung điểm CC’. Tính góc giữa hai đường thẳng AD’ và BM. A.
18
0
26
B.
45
0
C.
26
0
33
D.
18
0
43
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có các cạnh bằng 1. M là trung điểm CC’. Tính góc giữa hai đường thẳng AD’ và BM.
A. 18 0 26 '
B. 45 0
C. 26 0 33 '
D. 18 0 43 '
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM và DB’ A.
a
2
7
B.
a
4
C.
2
7
a
D.
a...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM và DB’
A. a 2 7
B. a 4
C. 2 7 a
D. a 2
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của cạnh SC. Xét điểm M thay đổi trên cạnh AB. Giá trị nhỏ nhất của độ dài đoạn thẳng MI bằng A.
a
7
2
B.
a
3
C.
a
5
2
D. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của cạnh SC. Xét điểm M thay đổi trên cạnh AB. Giá trị nhỏ nhất của độ dài đoạn thẳng MI bằng
A. a 7 2
B. a 3
C. a 5 2
D. a 2
Cho hình lập phương
ABCD
.
A
B
C
D
có cạnh bằng a. Một đường thẳng d đi qua đỉnh D¢ và tâm I của mặt bên
BCC
B
.
Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng
BCC
B
và
ABCD
sao cho trung điểm K của MN thuộc đường thẳn...
Đọc tiếp
Cho hình lập phương ABCD . A ' B ' C ' D ' có cạnh bằng a. Một đường thẳng d đi qua đỉnh D¢ và tâm I của mặt bên BCC ' B ' . Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng BCC ' B ' và ABCD sao cho trung điểm K của MN thuộc đường thẳng d (tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là
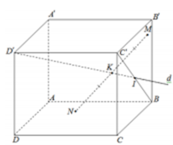
A. 3 a 2
B. 3 5 a 10
C. 2 5 a 5
D. 2 3 a 5
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Điểm M thuộc tia DD’ thỏa mãn
D
M
a
6
. Góc giữa đường thẳng BM và mặt phẳng (ABCD) là A.
30
o
B.
45
o
C.
75
o
D.
60
o
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Điểm M thuộc tia DD’ thỏa mãn D M = a 6 . Góc giữa đường thẳng BM và mặt phẳng (ABCD) là
A. 30 o
B. 45 o
C. 75 o
D. 60 o
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB 1, AC 2; cạnh bên SA vuông góc với đáy và SA 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho
A
M
x
0
x
1
và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt phẳng (P) có diện tích lớn nhất thì giá trị của x bằng. A. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = 1, AC = 2; cạnh bên SA vuông góc với đáy và SA = 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho A M = x 0 < x < 1 và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt phẳng (P) có diện tích lớn nhất thì giá trị của x bằng.
A. 2 3
B. 3 4
C. 1 3
D. 1 2
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, độ dài cạnh bên bằng 2a. Xét điểm M thay đổi trên mặt phẳng (SAB) sao cho tổng
T
M
A
2
+
M
B
2
+
M
C
2
+
M
D
2
nhỏ nhất. Khi đó, độ dài đoạn thẳng SM bằng A.
7
a...
Đọc tiếp
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, độ dài cạnh bên bằng 2a. Xét điểm M thay đổi trên mặt phẳng (SAB) sao cho tổng T = M A 2 + M B 2 + M C 2 + M D 2 nhỏ nhất. Khi đó, độ dài đoạn thẳng SM bằng
A. 7 a 15 15
B. a 15 2
C. a 15 3
D. 4 a 15 15
Trong không gian với hệ tọa độ Oxyz, cho điểm A( 1; 2;-3) và mặt phẳng(P):2x+2y-z+90. Đường thẳng d đi qua A và có véctơ chỉ phương
u
⇀
(3;4;-4) cắt (P) tại B. Điểm M thay đổi trong (P) sao cho M luôn nhìn đoạn AB dưới góc
90
°
. Khi độ dài MB lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau?
A
.
H
(
-
2
;
-
1
;
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A( 1; 2;-3) và mặt phẳng(P):2x+2y-z+9=0. Đường thẳng d đi qua A và có véctơ chỉ phương u ⇀ =(3;4;-4) cắt (P) tại B. Điểm M thay đổi trong (P) sao cho M luôn nhìn đoạn AB dưới góc 90 ° . Khi độ dài MB lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau?
A . H ( - 2 ; - 1 ; 3 )
B . I ( - 1 ; - 2 ; 3 )
C . K ( 3 ; 0 ; 15 )
D . J ( - 3 ; 2 ; 7 )