\(A'C'=\sqrt{a^2+a^2}=a\sqrt{2}\)
=>\(A'C=\sqrt{\left(a\sqrt{2}\right)^2+\left(a\sqrt{3}\right)^2}=a\sqrt{5}\)
\(A'C'=\sqrt{a^2+a^2}=a\sqrt{2}\)
=>\(A'C=\sqrt{\left(a\sqrt{2}\right)^2+\left(a\sqrt{3}\right)^2}=a\sqrt{5}\)
Cho hình lập phương ABCD. A'B'C'D' cạnh a. Tính khoảng cách từ B tới đường thẳng DB'.
A. a 3 6
B. a 6 3
C. a 3 3
D. a 6 6
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính thể tích khối nón có đỉnh là tâm hình vuông ABCD và đáy là đường tròn nội tiếp hình vuông A'B'C'D'
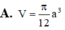
![]()
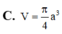
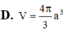
cho hình lập phương ABCD.A'B'C'D' và M,N,E,F lần lượt là trung điểm các cạnh BC, BA, AA' , A'D'. Tính góc giữa các cặp đường thẳng sau
a) A'C' và BC
b) MN và EF
c) MN và BC
d) EF và CC'
Cho hình lập phương ABCD. A'B'C'D'. Góc giữa hai đường thẳng BA' và CD bằng
A. 45 °
B. 60 °
C. 30 °
D. 90 °
Cho hình lập phương ABCD. A'B'C'D'. Khẳng định nào sau đây là khẳng định sai?
A. Góc giữa hai đường thẳng B’D’ và AA’ bằng 60 ⁰
B. Góc giữa hai đường thẳng AC và B’D’ bằng 90 ⁰
C. Góc giữa hai đường thẳng AD và B’C bằng 45 ⁰
D. Góc giữa hai đường thẳng BD và A’C’ bằng 90 ⁰
Cho hình hộp ABCD A B C D . A'B C'D ' có :
AB=1, AD=2, A A'=3. Góc BAD =120 độ, BAA= 60 độ , DAA=60 độ . Gọi I là giao điểm của BC' và BC' . 1) Tính các tích sau AB .AD ,AB. AA' ,AD. AA'. 2) Tính AI AC . 3) Tính AI . 4) Tính góc giữa AI và AC'.Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2a Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A'B'C'D' Diện tích S là
![]()
![]()
![]()
![]()
Cho hình hộp chữ nhật ABCD. A’B’C’D’có AB = a, BC = 2a, AA’ = a. Lấy điểm I trên cạnh AD sao cho AI = 3 ID. Tính thể tích của khối chop B’. IAC.
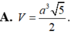
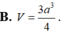
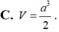
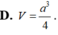
Cho hình lập phương ABCD. A ‘B’C’D’ có độ dài cạnh bằng 1. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, C’D’ và DD’. Tính thể tích khối tứ diện MNPQ
A. 3 8
B. 1 8
C. 1 12
D. 1 24