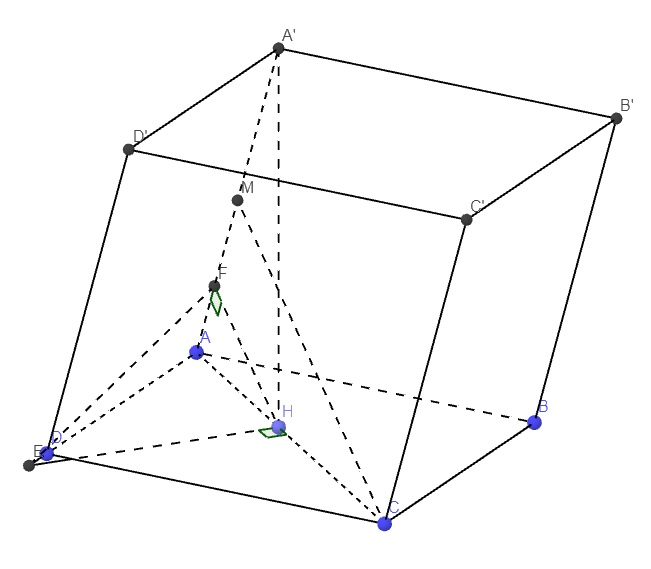
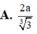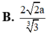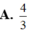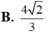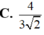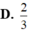Kẻ \(A'H\perp AC\Rightarrow A'H\perp\left(ABCD\right)\)
Kẻ \(HF\perp A'A\), trong mp (ABCD) qua H kẻ đường thẳng vuông góc AC cắt AD kéo dài tại E
\(\Rightarrow A'A\perp\left(EFH\right)\Rightarrow\widehat{EFH}\) là góc giữa (ACC'A') và (ADD'A')
\(\Rightarrow tan\widehat{EFH}=\dfrac{EH}{FH}=\dfrac{3}{2}\) (1)
Hai tam giác vuông AHE và ADC đồng dạng (chung góc A)
\(\Rightarrow\dfrac{HE}{CD}=\dfrac{AH}{AD}\Rightarrow\dfrac{EH}{AH}=\dfrac{CD}{AD}=\sqrt{2}\) (2)
(1);(2) \(\Rightarrow\dfrac{FH}{AH}=\dfrac{2\sqrt{2}}{3}=sin\widehat{A'AH}\)
\(AC=\sqrt{AB^2+AD^2}=3=A'C\Rightarrow\Delta A'AC\) cân tại C
Gọi M là trung điểm \(A'A\Rightarrow CM\perp A'A\Rightarrow CM||FH\)
\(\Rightarrow\dfrac{CM}{AC}=\dfrac{FH}{AH}=\dfrac{2\sqrt{2}}{3}\Rightarrow CM=2\sqrt{2}\)
\(\Rightarrow AM=\sqrt{AC^2-CM^2}=1\Rightarrow A'A=2\)
\(\Rightarrow A'H=A'A.sin\widehat{A'AH}=\dfrac{4\sqrt{2}}{3}\)
\(\Rightarrow V=A'H.AB.AD=8\)






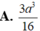
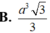
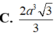
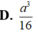
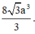 Tính độ dài đoạn thẳng AC.
Tính độ dài đoạn thẳng AC.