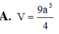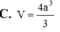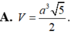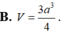Question

cho hình hộp chữ nhật ABCD.A'B'C'D' có cạnh AB = 2a, BC = 3a, AA' = 4a

a) tính d(B'B,AD)

b) tính d(B'D',AC)

Answer 1

a.

Theo t/c hình hộp chữ nhật: \(\left\{{}\begin{matrix}AB\perp BB'\\AB\perp AD\end{matrix}\right.\)

\(\Rightarrow AB\) là đoạn vuông góc chung của BB' và AD

\(\Rightarrow d\left(B'B;AD\right)=AB=2a\)

b.

Gọi O, O' lần lượt là tâm ABCD và A'B'C'D'

\(\Rightarrow OO'=AA'=4a\)

\(OO'||AA'\Rightarrow\left\{{}\begin{matrix}OO'\perp B'D'\\OO'\perp AC\end{matrix}\right.\)

\(\Rightarrow d\left(B'D',AC\right)=OO'=4a\)