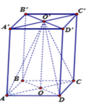
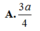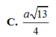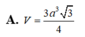Ta có:
\(\widehat{A'AD}=\widehat{A'AB}=120^0\)
\(\Rightarrow\widehat{AA'D'}=\widehat{AA'B'}=60^0\)
\(\widehat{B'A'D'}=\widehat{BAD}=60^0\)
Kết hợp giả thiết các cạnh của hình hộp đã cho có độ dài bằng 1 ta có tứ diện \(AA'B'D'\) đều, cạnh 1
Gọi H là tâm của \(\Delta A'B'D'\)\(\Rightarrow AH\perp\left(A'B'C'D'\right)\)
\(AH=\dfrac{\sqrt{6}}{3}\); \(HC'=\dfrac{2\sqrt{3}}{3};OH=\dfrac{\sqrt{3}}{6}\) \(\Rightarrow AC'=\sqrt{AH^2+HC'^2}=\sqrt{2}\)
\(AO=\sqrt{AH^2+OH^2}=\dfrac{\sqrt{3}}{2}\)