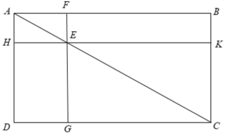
Theo giả thiết ta có FG//AD, HK//AB nên HE//AF và AH//EF.
Xét tứ giác AFEH có:
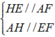 ⇒ AFEH là hình bình hành.
⇒ AFEH là hình bình hành.


Theo giả thiết ta có FG//AD, HK//AB nên HE//AF và AH//EF.
Xét tứ giác AFEH có:
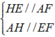 ⇒ AFEH là hình bình hành.
⇒ AFEH là hình bình hành.

Cho hình 125 trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD và HK // AB. Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích.
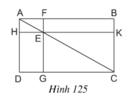
Bài 1: cho hình chữ nhật ABCD. E là điểm bất kì trên đường chéo AC. đường thẳng qua E, song song với AD cắtt AB, DC lần lượt tại F, G. đường thẳng qua E, song song với AB cắt AD, BC lần lượt tại H, K. chứng minh 2 hình chữ nhật EFBK và EGDH có cùng diện tích
Cho ABCD là hình chữ nhật trong đó E là điểm bất kỳ nằm trên đường chéo AC, FG // AD , HK // AB. Chứng minh diện tích EFBK = diện tích EGDH.
Ai giải giúp mình bài 13 sgk lớp 8 trang 119 mình cần gấp
Đề: Cho hình 125,trong đó ABCD là hình chữ nhật,E là một điểm bất kì nằm trên đường chéo AC,FG//AD và HK//AB.Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích
Cho hình thoi ABCD và điểm M bất kỳ thuộc đường chéo AC. Đường thẳng qua M song song vói AB cắt AD ở E, BC ở G. Đường thẳng qua M song song với AD cắt AB ở F, DC ở H.
a) Các Tứ giác AEMF và MHCG là hình gì ?
b) Tứ giác EFGH là hình gì?
c) Tìm vị trí của M trên AC để EFGH là hình chữ nhật.
d) Chứng minh rằng diện tích tứ giác EFGH không đổi khi M chuyển động trên đường chéo AC
Cho hình 125, trong đó ABCD là hình chữ nhật, E là một điểm bất kì nằm trên đường chéo AC, FG // AD, và HK // AB.
Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại h và K. Chứng minh rằng:
a) Tứ giác AHFK là hình chữ nhật;
b) AF song song với BD;
c) Ba điểm E, H, K thẳng hàng
Cho hình chữ nhật ABCD có O là giao điểm hai đường chéo AC và BD . Lấy điểm
P trên cạnh BD ( P nằm giữa O và D ). Gọi M là điểm đối xứng với C qua P .
a) Chứng minh AMDB là hình thang. Xác định vị trí điểm P trên BD để AMBD
là hình thang cân.
b) Kẻ ME AD MF AB , . Chứng minh rằng EF AC // và E F P , , thẳng hàng.
c) Trên cạnh AB lấy điểm X , trên DC lấy điểm J sao cho AX CJ lấy N là
điểm tùy ý trên AD . Gọi G là giao điểm của XJ và NB , H là giao điểm của XJ và
NC . Tính diện tích của tứ giác AXJD theo S S ABCD . Chứng minh rằng
S S S AXGN NHJD GBCH
Cho hình chữ nhật ABCD. O là giao điểm hai đường chéo và một điểm P bất kì trên đường chéo BD (P nằm giữa O và D). Gọi M là điểm đối xứng của C qua P. a) Chứng minh tứ giác AMDB là hình thang. Xác định vị trí của P trên BD để AMDB là hình thang cân. b) Kẻ ME vuông góc AD, MF vuông góc BA. Chứng minh EF // AC và 3 điểm E, F, P thẳng hàng. c) Xác định vị trí P trên BD để tứ giác nối 4 điểm A, M, D, B là hình thang cân. d) Nếu hình chữ nhật ABCD có AB = 2BC. Gọi K là điểm trên AB sao cho góc ADK = $15^o$. Chứng minh tam giác CDK cân.