Các câu hỏi tương tự
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh 2a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N lần lượt là trung điểm của BC và CD. Khi đó bán kính mặt cầu ngoại tiếp khối SCMN là: A.
3
a
2
B.
a
3
C.
93
6
a
D.
31
12
a
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh 2a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N lần lượt là trung điểm của BC và CD. Khi đó bán kính mặt cầu ngoại tiếp khối SCMN là:
A. 3 a 2
B. a 3
C. 93 6 a
D. 31 12 a
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AD 2a, AB a, cạnh bên SA
a
2
và vuông góc với mặt phẳng đáy (ABCD). Gọi M là trung điểm của cạnh BC. Tính bán kính hình cầu ngoại tiếp hình chóp S.AMD A.
a
6
6
B.
a
6
4
C.
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AD = 2a, AB = a, cạnh bên SA = a 2 và vuông góc với mặt phẳng đáy (ABCD). Gọi M là trung điểm của cạnh BC. Tính bán kính hình cầu ngoại tiếp hình chóp S.AMD
A. a 6 6
B. a 6 4
C. a 6 2
D. a 6 3
Cho hình chữ nhất ABCD có cạnh AB 6, AD 4. Gọi M, N, P, Q lần lượt là trung điểm bốn cạnh AB, BC, CD, DA. Cho hình chữ nhất ABCD quay quanh QN, khi đó tứ giác MNPQ tạo thành vật tròn xoay có thể tích bằng
A
.
4
π
B
.
8
π
C
.
10
π
D
.
24
π
Đọc tiếp
Cho hình chữ nhất ABCD có cạnh AB = 6, AD = 4. Gọi M, N, P, Q lần lượt là trung điểm bốn cạnh AB, BC, CD, DA. Cho hình chữ nhất ABCD quay quanh QN, khi đó tứ giác MNPQ tạo thành vật tròn xoay có thể tích bằng
A . 4 π
B . 8 π
C . 10 π
D . 24 π
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB2a, BCa. Các cạnh bên của hình chóp bằng nhau và bằng
a
2
. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho KD2KA. Tính khoảng cách giữa hai đường thẳng MN và SK. A.
3
a
2
B.
a
2
3
C. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=2a, BC=a. Các cạnh bên của hình chóp bằng nhau và bằng a 2 . Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho KD=2KA. Tính khoảng cách giữa hai đường thẳng MN và SK.
A. 3 a 2
B. a 2 3
C. a 3 7
D. a 21 7
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M và N lần lượt là trung điểm của BC và CD. Bán kính của mặt cầu ngoại tiếp hình chóp S.CMN là: A.
a
93
12
B.
a
29
8
C.
5
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M và N lần lượt là trung điểm của BC và CD. Bán kính của mặt cầu ngoại tiếp hình chóp S.CMN là:
A. a 93 12
B. a 29 8
C. 5 a 3 12
D. a 37 6
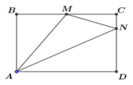
Trong mặt phẳng tọa độ oxy Cho hình vuông ABCD có A (-2,0) điểm C nằm trên đường thẳng có pt X+Y-3=o ,M là trung điểm cạnh BC N nằm trên AD sao cho AN = 2 ND .tìm tọa đôj B,C,D .biết phương trình MN 7X-6Y-5=0
Cho hình chữ nhật ABCD có cạnh AB=4,AD=6. Gọi M,N lần lượt là trung điểm của AD,BC. Tính thể tích hình trụ tròn xoay được tạo thành khi quay hình chữ nhật ABCD quanh cạnh MN.
A. 36π
B. 12π
C. 24π
D. 18π
Cho hình chữ nhật ABCD có cạnh
AB
4
,
AD
6
. Gọi M, N lần lượt là trung điểm của AD, BC. Tính thể tích hình trụ tròn xoay được tạo thành khi quay hình chữ nhật ABCD quanh cạnh MN. A.
18
π
B.
12
π
C.
36
π
D.
24
π
Đọc tiếp
Cho hình chữ nhật ABCD có cạnh AB = 4 , AD = 6 . Gọi M, N lần lượt là trung điểm của AD, BC. Tính thể tích hình trụ tròn xoay được tạo thành khi quay hình chữ nhật ABCD quanh cạnh MN.
A. 18 π
B. 12 π
C. 36 π
D. 24 π
Trong không gian cho ABCD là hình chữ nhật, AB2, AD1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết
d
(
A
B
,
d
)
d
(
C
D
,
d
)
. Tính a biết rằng thể t...
Đọc tiếp
Trong không gian cho ABCD là hình chữ nhật, AB=2, AD=1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d ( A B , d ) < d ( C D , d ) . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
A. a = 3
B. a = - 1 + 2
C. a = 1 2
D. a = 15 2