Đáp án B
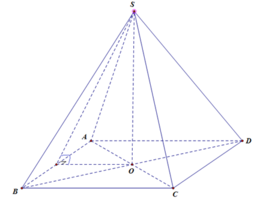
Ta có
S A B , A B C D ^ = S H O ^ = α ⇒ O H = h tan α ⇒ A D = 2 h tan α
Thể tích khối chóp S . A B C D là
V S . A B C D = 1 3 . S A B C D . h = 1 3 2 h tan α 2 . h = 4 h 3 3 tan 2 α
Đáp án B

Ta có
S A B , A B C D ^ = S H O ^ = α ⇒ O H = h tan α ⇒ A D = 2 h tan α
Thể tích khối chóp S . A B C D là
V S . A B C D = 1 3 . S A B C D . h = 1 3 2 h tan α 2 . h = 4 h 3 3 tan 2 α
Cho hình chóp tứ giác đều S.ABCD có AB = a, gọi α là góc giữa mặt bên và mặt đáy của hình chóp S.ABCD. Tính khoảng cách d giữa SA và CD theo a và α
A. d = a.cos α
B. d = a.sin α
C. d = a.sin2 α
D. d = a.cos2 α
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a, góc giữa mặt bên và mặt phẳng đáy là α thỏa mãn cos α = 1 3 . Mặt phẳng (P) qua AC và vuông góc với mặt phẳng (SAD) chia khối chóp S.ABCD thành hai khối đa diện. Tỷ số thể tích của hai khối đa diện (khối bé chia khối lớn) bằng
A. 1 9
B. 1 10
C. 7 9
D. 9 10
Cho khối chóp tứ giác đều S.ABCD có cạnh bên bằng a, mặt bên tạo với đáy một góc bằng α . Khi thể tích khối chóp S.ABCD tính theo a và đạt giá trị lớn nhất, chọn khẳng định đúng
A. α ∈ 30 0 ; 60 0
B. α ∈ 0 0 ; 45 0
C. α ∈ 60 0 ; 90 0
D. α ∈ 45 0 ; 60 0
Cho khối chóp tứ giác đều S.ABCD có thể tích bằng a 3 và đáy ABCD là hình vuông cạnh a. Tính cosα với α là góc giữa mặt bên và mặt đáy
A. cos α = 1 5
B. cos α = 1 3
C. cos α = 1 37
D. cos α = 1 19
Cho khối chóp tứ giác đều S.ABCD, gọi α mặt phẳng qua A và vuông góc SC.
Biết rằng diện tích thiết diện tạo bởi α là hình chóp bằng nửa diện tích đáy ABCD. Tính
góc φ tạo bởi cạnh bên SC và mặt đáy.
A. φ = arcsin 1 + 33 8
B. φ = arcsin 33 − 1 8
C. φ = arcsin 1 + 29 8
D. φ = arcsin 29 − 1 8
Cho hình chóp S.ABCD có các cạnh bên bằng a, góc hợp bởi đường cao SH của hình chóp và các mặt bên của hình chóp đều bằng α ( α thay đổi). Tìm giá trị lớn nhất của thể tích của S.ABCD?
A. 2 a 3 3 3
B. 2 a 3 9 3
C. 4 a 3 3 3
D. Đáp án khác
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của BC, SA, α là góc tạo bởi đường thẳng EM và mặt phẳng (SBD), tan α bằng:
A. 1
B. 2
C. 2
D. 3
Cho hình chóp S . A B C D có đáy ABCD là hình vuông cạnh 2a. Gọi O là giao điểm của AC và BD. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng A B C D là trung điểm H của đoạn OA và S D , A B C D = 60 ∘ . Gọi α là góc giữa hai mặt phẳng S C D v à A B C D . Tính t a n α .
A. t a n α = 4 15 9
B. tan α = 30 12
C. tan α = 10 3
D. tan α = 30 3
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA, α là góc tạo bởi đường thẳng EM và mặt phẳng S B D , tan α bằng
A. 2
B. 3
C. 2
D. 1